Image Inpainting

(持续更新中…)

TELEA

原论文下载；带笔记论文下载
这个算法是opencv自带的图像修复算法，直接说算法的流程吧：

1.区域划分

把每个像素标记为KNOWN、BAND、INSIDE三种

INSIDE：待修复的像素，表示是待修复的块的内部像素。
BAND：与待修复的像素相邻的已知像素，表示块的边界。
KNOWN：其他已知像素。

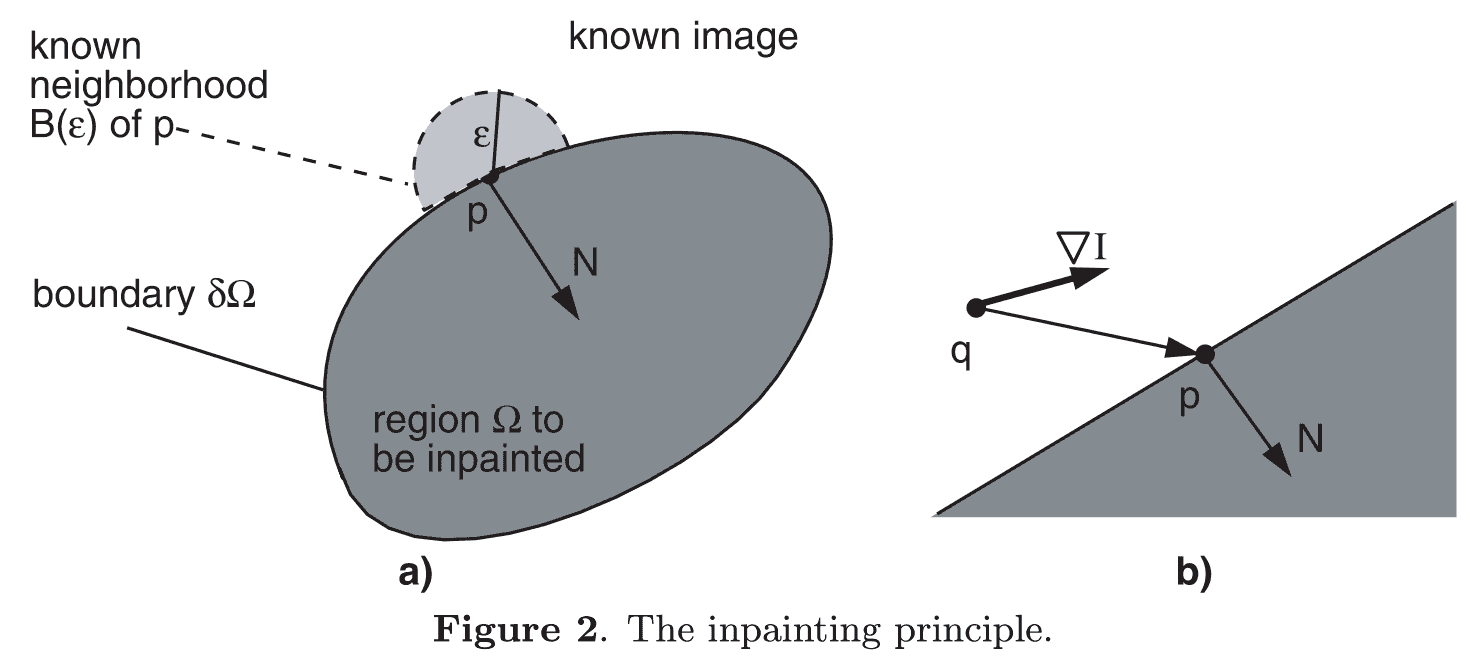
如上图(a)所示，圈内是待修复部分INSIDE，圈外是已知部分KNOWN，圈就是BAND。

2.修复单个像素

考虑修复一个与BAND相邻的未知点 \(p\)，如上图(b)所示，对于附近某一个已知(BAND和KNOWN)的点 \(q\)，可以通过 \(I(p)=I(q)+\nabla I(q)*(p-q)\) 来预测待修复点 \(p\)。
基于这个思路，可以以 \(p\) 为圆心 \(\varepsilon\) 为半径画一个圆，如上图(a)，圆内已知像素集合记为 \(B_\varepsilon(p)\)，对于任意 \(q\in B_\varepsilon\) 都会对 \(I(p)\) 有一个预测值，对每一个预测赋予合适的权值 \(w(p,q)\)，最后用归一化加权预测结果作为像素修复的值，且此后将像素视为已知，继续修复下一个像素。

\[I(p)=\frac{\underset{q\in B_\varepsilon(p)}{\sum}w(p,q)[I(q)+\nabla I(q)(p-q)]}{\underset{q\in B_\varepsilon(p)}{\sum} w(p,q)}\]

3.修复顺序

前面已经提到是一个一个像素修复，而顺序则是沿着边界往中心蔓延挨个修复。
令 \(T(p)\) 表示像素 \(p\) 离BAND的最近距离，就可以通过 \(T(p)\) 从小到大修复未知的像素。（\(T\) 相等的点连起来可看做等高线）
\(T(p)\) 通过求解下面方程得到，实际上不是严格的距离。

\[\vert\nabla T\vert=1,\quad with\; T=0\; in\; BAND\]

数值求解方法如下：

\[\max(D^{-x}T,-D^{+x}T,0)^2+\max(D^{-y}T,-D^{+y}T,0)^2=1\]

其中：(\(D^{\pm y}\) 类似)

\[D^{-x}T(i,j)=T(i,j)-T(i-1,j)\] \[D^{+x}T(i,j)=T(i+1,j)-T(i,j)\]

令 \(T_0=T(i,j),T_1=T(i+\Delta i,j),T_2=T(i,j+\Delta j)\)，则有：

\[\begin{aligned} (T_0-T_1)^2+(T_0-T_2)^2=&1\\ 2T_0^2-2(T_1+T_2)T_0+T_1^2+T_2^2-1=&0\\ \end{aligned}\]

解一元二次方程得：

\[T_0=\frac{(T_1+T_2)\pm\sqrt{(2-(T_1-T_2)^2)}}{2}\]

通过上面的更新距离方法，再结合最短路算法SPFA可以得到所有\(T\)值（这种结合可能不太严谨，但是无伤大雅）
此时对于KNOWN类型的点将 \(T\) 取反，这样通过 \(T\) 相减就有等高线差值的意义了。
最后使用 \(3\times 3\; \mathrm{tent}\; \mathrm{filter}\) 处理 \(T\)，在网上查了一下这里的 \(\mathrm{tent}\; \mathrm{filter}\) 可能是指如下函数：

\[f(x)=\left\{ \begin{aligned} 1-\vert x\vert, \vert x\vert\leq 1\\ 0, \vert x\vert >1 \end{aligned} \right.\]

扩展到二维我在代码里直接用的3*3高斯核。

4.权值设置

考虑待修复点 \(p\) 及已知点 \(q\in B_\varepsilon(p)\)

1.方向部分：\(\nabla T\) 的方向如果和 \((p-q)\) 的方向一致，则给予更大权重，设置为两者的点积。

\[dir(p,q)=\frac{p-q}{\parallel p-q\parallel}\cdot \nabla T\]

2.距离部分：\(p\) 和 \(q\) 距离越远，权重越小，设置为距离平方的倒数

\[dst(p,q)=\frac{d_0^2}{\parallel p-q\parallel^2}\]

3.等高线部分：\(T(p)\) 和 \(T(q)\) 差距越大，权重越小

\[lev(p,q)=\frac{T_0}{1+\vert T(p)-T(q)\vert}\]

权重则设置为三者乘积

\[w(p,q)=dir(p,q)*dst(p,q)*lev(p,q)\]

实验结果

（一开始想着熟悉C++的优先队列就用C++实现，现在想想真是脑抽，写完加调试花了大概十个小时，Matlab它不香吗
自己写的效果和opencv自带函数相比有一定的差距，可能代码还有小bug或者具体实现和作者还有点出入，但是已经不想折腾了。
从左到右分别是原图，opencv结果，我自己写的代码结果。(代码见附录)

附录

#include "opencv2/imgproc.hpp"

#include "opencv2/highgui.hpp"

#include "opencv2/photo.hpp"


#include<cmath>

#include<queue>

#include<cstdio>

#include<cstring>

#include<cstdlib>

#include<iostream>

#include<algorithm>


using namespace std;
using namespace cv;

#define KNOWN 0

#define BAND 1

#define INSIDE 2


#define epsilon 6


#define X first

#define Y second


const int To[4][2] = { {1,0}, {-1,0}, {0,1}, {0,-1} };

int B[epsilon * epsilon * 4 + 1][2];
int Btop = -1;

string img_path = "/home/chongjg/Desktop/image-inpainting/image/";
string output_path = "/home/chongjg/Desktop/image-inpainting/output/";

Mat img, mask;

int N, M;

char* f;
float* T;
bool* vis;

bool Check(int i, int j){ return 0 <= i && i < N && 0 <= j && j < M; }

void create_mask(Mat &img, string &img_path){
    int width = 30;
    int interval = 3;
    mask = Mat(img.rows, img.cols, CV_8UC1);
    for(int i = 0; i < img.rows; i ++)
        for(int j = 0; j < img.cols; j ++)
            mask.at<uchar>(i, j) = (((i / width) % interval == 0) & ((j / width) % interval == 0)) * 255;
    imwrite(img_path + "mask.jpg", mask);
}

struct BandPixel{

    float T;
    int x, y;

    BandPixel(){}
    BandPixel(float T, int x, int y) : T(T), x(x), y(y) {}

};

bool operator < (const BandPixel &a, const BandPixel &b){return a.T > b.T;}

float solEqua(int i1, int j1, int i2, int j2){
    static float r, s, T1, T2;
    float re = 1e6;
    if(!Check(i1, j1) || !Check(i2, j2))
        return re;
    T1 = T[i1 * M + j1], T2 = T[i2 * M + j2];
    if(T1 < 1e6){
        if(T2 < 1e6){
            r = sqrt(2 - (T1 - T2) * (T1 - T2));
            s = (T1 + T2 - r) / 2;
            if(s >= max(T1, T2))
                re = s;
            else if(s + r >= max(T1, T2))
                re = s + r;
        }
        else
            re = 1 + T1;
    }
    else if(T2 < 1e6)
        re = 1 + T2;
    return re;
}

void TentFilter(){
    const int kernal[] = {1, 2, 1, 2, 4, 2, 1, 2, 1};
    const int idx[9][2] = { {-1,-1}, {-1,0}, {-1,1}, {0,-1}, {0,0}, {0,1}, {1,-1}, {1,0}, {1,1} };
    float* tmp = new float[N * M];
    memset(tmp, 0, sizeof(float) * N * M);
    int ii, jj, w;
    for(int i = 0; i < N; i ++)
        for(int j = 0; j < M; j ++){
            w = 0;
            for(int k = 0; k < 9; k ++){
                ii = i + idx[k][0];
                jj = j + idx[k][1];
                if(Check(ii, jj))
                    w += kernal[k], tmp[i * M + j] += kernal[k] * T[ii * M + jj];
            }
            tmp[i * M + j] /= w;
        }
    for(int i = 0; i < N * M; i ++)
        T[i] = tmp[i];
}

priority_queue<BandPixel> NarrowBand;
queue<pair<int, int> > ToBeInpainted;

void Init(){
    int i, j;
    
    //initiate B

    for(i = -epsilon; i <= epsilon; i ++)
        for(j = -epsilon; j <= epsilon; j ++)
            if(i * i + j * j <= epsilon * epsilon){
                Btop ++;
                B[Btop][0] = i;
                B[Btop][1] = j;
            }

    // input image & mask
    
    img = imread(img_path + "test.jpg");
    create_mask(img, img_path);

    N = img.rows;
    M = img.cols;

    // initiate f
    
    f = new char[N * M];
    memset(f, KNOWN, sizeof(char) * N * M);

    for(i = 0; i < N; i ++)
        for(j = 0; j < M; j ++){
            if(mask.at<uchar>(i, j) == 0)
                continue;
            f[i * M + j] = INSIDE;
            for(int k = 0; k < 4; k ++){
                int ii = i + To[k][0], jj = j + To[k][1];
                if(Check(ii, jj) && f[ii * M + jj] == KNOWN)
                    f[ii * M + jj] = BAND;
            }
        }

    // initiate NarrowBand & T

    BandPixel t;

    T = new float[N * M];
    memset(T, 0, sizeof(float) * N * M);

    for(i = 0; i < N; i ++)
        for(j = 0; j < M; j ++)
            if(f[i * M + j] == BAND)
                NarrowBand.push(BandPixel(T[i * M + j], i, j));
            else
                T[i * M + j] = 1e6;

    bool *vis = new bool[N * M];
    memset(vis, false, sizeof(bool) * N * M);

    while(!NarrowBand.empty()){
        t = NarrowBand.top();
        NarrowBand.pop();
        i = t.x, j = t.y;
        if(vis[i * M + j])
            continue;
        vis[i * M + j] = true;
        ToBeInpainted.push(make_pair(i, j));
        for(int k = 0; k < 4; k ++){
            int ii = i + To[k][0], jj = j + To[k][1];
            if(!Check(ii, jj))
                continue;
            float tmpT = min(min(solEqua(ii - 1, jj, ii, jj - 1),
                                 solEqua(ii + 1, jj, ii, jj - 1)),
                             min(solEqua(ii - 1, jj, ii, jj + 1),
                                 solEqua(ii + 1, jj, ii, jj + 1)));
            tmpT = min(tmpT, T[i * M + j] + 1);
            if(tmpT < T[ii * M + jj]){
                T[ii * M + jj] = tmpT;
                NarrowBand.push(BandPixel(T[ii * M + jj], ii, jj));
            }
        }
    }

    for(i = 0; i < N; i ++)
        for(j = 0; j < M; j ++)
            if(f[i * M + j] == KNOWN)
                T[i * M + j] *= -1;
    
    TentFilter();
    
}

pair<float, float> GradT(int x, int y){
    static pair<float, float> re;
    if(x + 1 >= N)
        re.X = (T[x * M + y] - T[(x - 1) * M + y]);
    else if(x - 1 < 0)
        re.X = (T[(x + 1) * M + y] - T[x * M + y]);
    else
        re.X = (T[(x + 1) * M + y] - T[(x - 1) * M + y]) / 2;
    if(y + 1 >= M)
        re.Y = (T[x * M + y] - T[x * M + y - 1]);
    else if(y - 1 < 0)
        re.Y = (T[x * M + y + 1] - T[x * M + y]);
    else
        re.Y = (T[x * M + y + 1] - T[x * M + y - 1]) / 2;
    return re;
}

pair<Vec3f, Vec3f> GradI(int x, int y){
    static pair<Vec3f, Vec3f> re;
    for(int k = 0; k < 3; k ++){
        if(x + 1 >= N || f[(x + 1) * M + y] == INSIDE)
            if(x - 1 < 0 || f[(x - 1) * M + y] == INSIDE)
                re.X[k] = 0;
            else
                re.X[k] = ((float)img.at<Vec3b>(x, y)[k] - img.at<Vec3b>(x - 1, y)[k]);
        else if(x - 1 < 0 || f[(x - 1) * M + y] == INSIDE)
            re.X[k] = ((float)img.at<Vec3b>(x + 1, y)[k] - img.at<Vec3b>(x, y)[k]);
        else
            re.X[k] = ((float)img.at<Vec3b>(x + 1, y)[k] - img.at<Vec3b>(x - 1, y)[k]) / 2;
        if(y + 1 >= M || f[x * M + y + 1] == INSIDE)
            if(y - 1 < 0 || f[x * M + y - 1] == INSIDE)
                re.Y[k] = 0;
            else
                re.Y[k] = ((float)img.at<Vec3b>(x, y)[k] - img.at<Vec3b>(x, y - 1)[k]);
        else if(y - 1 < 0 || f[x * M + y - 1] == INSIDE)
            re.Y[k] = ((float)img.at<Vec3b>(x, y + 1)[k] - img.at<Vec3b>(x, y)[k]);
        else
            re.Y[k] = ((float)img.at<Vec3b>(x, y + 1)[k] - img.at<Vec3b>(x, y - 1)[k]) / 2;
    }
    return re;
}

void inpaint(int x, int y){
    static int i, j;
    static pair<int, int> r;
    static pair<float, float> gradT;
    static pair<Vec3f, Vec3f> gradI;
    static float dir, dst, lev, w;
    Vec3f Ia(0, 0, 0);
    float s = 0;
    gradT = GradT(x, y);
    for(int t = 0; t <= Btop; t ++){
        i = x + B[t][0], j = y + B[t][1];
        if(!Check(i, j) || f[i * M + j] == INSIDE)
            continue;
        r = make_pair(B[t][0], B[t][1]);
        dir = fabs(r.X * gradT.X + r.Y * gradT.Y) / sqrt(r.X * r.X + r.Y * r.Y);
        dst = 1.0 / (r.X * r.X + r.Y * r.Y);
        lev = 1.0 / (1 + fabs(T[x * M + y] - T[i * M + j]));
        w = dir * dst * lev;

        gradI = GradI(i, j);
        Ia += w * ((Vec3f)img.at<Vec3b>(i, j) + (gradI.X * r.X + gradI.Y * r.Y));
        s += w;
    }
    img.at<Vec3b>(x, y) = (Vec3b)(Ia / s);
}

void Solve(){
    int i, j;
    pair<int, int> p;
    
    while(!ToBeInpainted.empty()){
        p = ToBeInpainted.front();
        ToBeInpainted.pop();
        i = p.X, j = p.Y;
        f[i * M + j] = KNOWN;
        for(int k = 0; k < 4; k ++){
            int ii = i + To[k][0], jj = j + To[k][0];
            if(Check(ii, jj) && f[ii * M + jj] == INSIDE){
                inpaint(ii, jj);
                f[ii * M + jj] = BAND;
            }
        }
    }
    
}

int main(){

    Init();
    Solve();

    imshow("output", img);
    imwrite(output_path + "inpainted.jpg", img);
    waitKey(1);

    Mat imgdst(img.rows, img.cols, CV_8UC3);

    inpaint(img, mask, imgdst, epsilon, INPAINT_TELEA);
    imshow("cv_inpaint", imgdst);
    imwrite(output_path + "cv_inpaint.jpg", imgdst);
    waitKey(0);

    return 0;
}

DIP大作业