-
数字图像处理课程图像去噪课堂展示总结,部分理解有点困难的算法没有进行记录,下面算法基本都是看一眼就能get到主要思想的经典算法。
-
若无特殊说明,\(S_{ij}\)是以\((i,j)\)为中心,宽\(m\),高\(n\)的矩形邻域。
问题定义
\[y=x+n\]- \(y\)是观察到的带噪图像,\(x\)是未知的无噪声图像,\(n\)是高斯白噪声。要通过已知的\(y\)求\(x\)的估计\(\hat x\)。
一、空间域滤波
1.均值派
1.1 算术均值
\[\hat x(i,j)=\frac{1}{mn}\sum_{(s,t)\in S_{ij}}y(s,t)\]1.2 几何均值
\[\hat x(i,j)=\Big [\prod_{(s,t)\in S_{ij}}y(s,t)\Big ]^{\frac{1}{mn}}\]1.3 高斯均值
- 通过高斯函数\(f(x,y)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2+y^2}{2\sigma^2}}\)给邻域\(S_{ij}\)每个像素赋予一个权重再进行加权平均,是一种改良版的均值滤波。(\(\frac{1}{W}\)是权值归一化参数)
- 常用的三阶、五阶高斯卷积核:
1.4 双边滤波
-
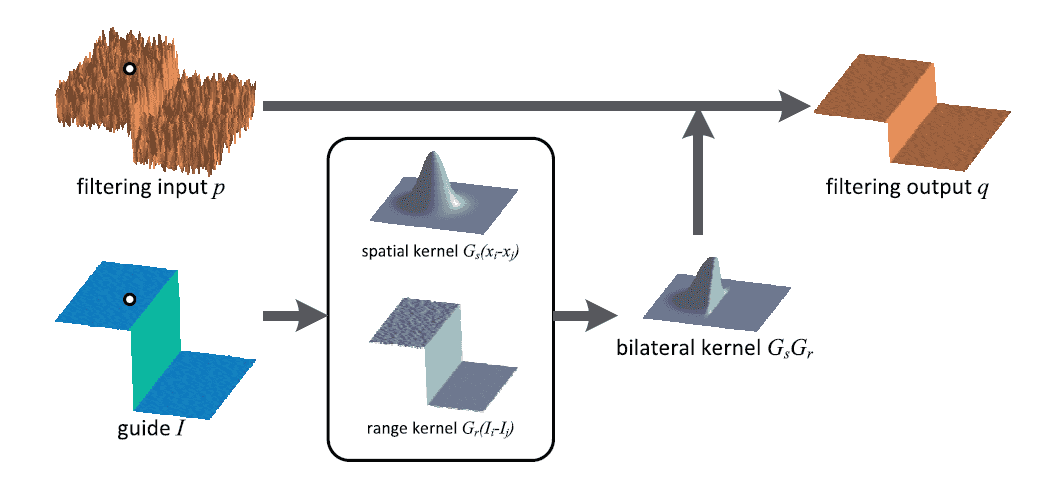
双边滤波可以理解为在高斯滤波的基础上进行的改进。高斯滤波在均值滤波的基础上考虑到离中心像素的距离越远,其影响也会越小,而双边滤波则在此基础上考虑到如果像素值差距很大,影响也应该较小。
-
举个例子,一张图片左边是黑色右边是白色,高斯滤波直接将边缘两侧差距巨大的像素无差别考虑,因此会在边界产生灰色边缘。而双边滤波由于异侧像素值差距较大会大大减小其影响从而更好地保留边缘特征。对于其他边缘原理相同,公式如下所示。(\(\frac{1}{W}\)是权重归一化参数)
1.5 谐波均值
\[\hat x(i,j)=\frac{mn}{\underset{(s,t\in S_{ij})}{\sum}\frac{1}{y(s,t)}}\]1.6 逆谐波均值
\[\hat x(i,j)=\frac{\underset{(s,t\in S_{ij})}{\sum}g(s,t)^{Q+1}}{\sum_{(s,t\in S_{ij})}g(s,t)^Q}\]1.7 递归均值
-
首先构造\(\mathbf B\)为\(01\)矩阵,0表示为噪声,1表示不是噪声。如果\(\mathbf B\)矩阵已知,那么这会是一个比较不错的算法。
-
然后看每一个噪声的4邻域,如果4邻域有超过2个为非噪声,则将原图这个噪声点像素值设置为4邻域的4次方平均值。
-
再看剩下噪声的8邻域,如果8邻域有超过2个为非噪声,则将原图这个噪声点像素设置为8邻域的8次方平均值。
-
当某次遍历没有噪声被修改,算法结束。
1.8 非局部均值
- 对任意像素\((i,j)\)有一个邻域窗口(比如\(7*7\)),窗口中每个块(比如\(3*3\))会有一个相较于中心块的相似度。设中心为\((i,j)\)的块为\(A\),对于邻域窗口中的一个中心为\((s,t)\)的块\(B\),其相似度\(S(s,t)\)定义如下(\(A_{m,n},B_{m,n}\)表示块内像素值)
- 则有
2.统计派
2.1 中值滤波
\[\hat x(i,j)=\underset{(s,t)\in S_{ij}}{\mathrm{median}}\{ y(s,t)\}\]2.2 最大值/最小值滤波
\[\hat x(i,j)=\underset{(s,t)\in S_{ij}}{\mathrm{max}}\{ y(s,t)\}\] \[\hat x(i,j)=\underset{(s,t)\in S_{ij}}{\mathrm{min}}\{ y(s,t)\}\]2.3 中点滤波
\[\hat x(i,j)=\frac{1}{2}\Big(\underset{(s,t)\in S_{ij}}{\mathrm{max}}\{ y(s,t)\}+\underset{(s,t)\in S_{ij}}{\mathrm{min}}\{ y(s,t)\}\Big)\]2.4 alpha剪枝均值
\[\hat x(i,j)=\frac{1}{mn-d}\underset{(s,t)\in S'_{ij}}{\sum}y(s,t)\]- \(\alpha-\)剪枝均值就是在原本的\(S_{ij}\)邻域内各删除灰度值最小和最大的\(\frac{d}{2}\)个点后求均值。
2.5 自适应中值滤波
- 通俗地说,就是如果\(y(i,j)\)在\(S_{ij}\)领域内既不是最大值也不是最小值,那么\(\hat x(i,j)=y(i,j)\),否则\(\hat x(i,j)\)为\(y\)的\(S_{ij}\)邻域的中值。
\(\hat x(i,j)=\left\{ \begin{aligned} &\underset{(s,t)\in S_{ij}}{\mathrm{median}}\{y(s,t)\} &y(i,j)=\underset{(s,t)\in S_{ij}}{\mathrm{min}}\{y(s,t)\}\ or\ \underset{(s,t)\in S_{ij}}{\mathrm{max}}\{y(s,t)\}\\ &y(i,j) &y(i,j)\neq \underset{(s,t)\in S_{ij}}{\mathrm{min}}\{y(s,t)\}\ or\ \underset{(s,t)\in S_{ij}}{\mathrm{max}}\{y(s,t)\}\\ \end{aligned} \right.\)
二、变换域滤波
1.傅里叶频域滤波
-
直接将\(y\)的频域图像\(Y\)对滤波器\(H\)进行矩阵点乘得到\(\hat x\)的频域图像\(\hat X\)。
-
令\(D(u,v)=(u^2+v^2)^\frac{1}{2}\)
1.1 低通滤波
- 理想低通滤波器:
\(H(u,v)=\left\{ \begin{aligned} &1 &if\ D(u,v)\leq D_0\\ &0 &otherwise\\ \end{aligned} \right.\)
- 巴特沃斯低通滤波器:
- 高斯低通滤波器:
1.2 带阻滤波
- 理想带阻滤波器:
- 巴特沃斯带阻滤波器:
- 高斯带阻滤波器:
1.3 高通、带通滤波
\[H_{HP}(u,v)=1-H_{LP}(u,v)\] \[H_{BP}(u,v)=1-H_{BR}(u,v)\]1.4 陷波滤波
- 通过移动高通滤波器的中心点,可以设计陷波滤波器(Notch filter)
- 上面是对频域中\((u_0,v_0)\)附近进行抑制,由于频域的对称性\((-u_0,-v_0)\)也要同样处理。如果要对多个点进行抑制,直接将滤波器相乘即可。
2.基于矩阵特征变换滤波
2.1 加权核范数最小化
-
(这个算法非常需要数学基础,如果要完全搞懂需要非常繁琐的证明,本人已放弃,有兴趣的可以看参考的5)
-
首先回忆线性代数的一些知识
-
矩阵的秩
\(\quad\quad\)矩阵的秩表示矩阵的所有行向量或所有列向量最多选出多少能组成线性无关组。也就是最多有多少行向量或列向量彼此都线性无关。矩阵的秩记作\(rank(\mathbf X)\),它也等于矩阵奇异值非零值的个数。
- 范数
\(\quad\) 1)向量范数(1-范数、2-范数、\(\infty\)-范数、p-范数)
\[\left\|x\right\|_1=\sum_{i=1}^N\vert x_i\vert\] \[\left\|x\right\|_2=\Big(\sum_{i=1}^N\vert x_i\vert^2\Big)^{\frac{1}{2}}\] \[\left\|x\right\|_{\infty}=\max_i\vert x_i\vert\] \[\left\|x\right\|_p=\Big(\sum_{i=1}^N\vert x_i\vert^p\Big)^{\frac{1}{p}}\]\(\quad\) 2)矩阵范数
\(\quad \quad\)1-范数:列向量每个元素绝对值之和的最大值
\[\left\|\mathbf X\right\|_1=\max_j\sum_{i=1}^N\vert\mathbf X_{i,j}\vert\]\(\quad \quad\)2-范数:奇异值的最大值,或者说是\(\mathbf{XX}^T\)特征值\(\lambda\)最大值开根号
\[\left\|\mathbf X\right\|_2=\max_i\sqrt{\lambda_i}\]\(\quad \quad\infty\)-范数:行向量每个元素绝对值之和的最大值
\[\left\|\mathbf X\right\|_{\infty}=\max_i\sum_{j=1}^N\vert\mathbf X_{i,j}\vert\]\(\quad\quad\)Frobenius范数:每个元素的平方的和开根号
\[\left\|\mathbf X\right\|_F=\sqrt{\sum_i\sum_j\mathbf X^2_{i,j}}\]\(\quad \quad\)核-范数:奇异值的和(奇异值分解),即\(\mathbf{XX}^T\)特征值开根号的和
\[\left\|\mathbf X\right\|_*=\sum_i\sqrt{\lambda_i}\]- 总之,该算法可以用于主成分分析、图像补全、图像去噪。全文基本都是围绕着如何解下面这一方程展开:
- \(\parallel\mathbf X\parallel_{\mathbf w,*}\)就是加权核范数。
- 论文中详细地介绍了权值\(\mathbf w\)如何定义、如何近似上述方程使得可以通过迭代求解等等。但是数学证明及转化对我来说过于复杂,遂放弃。
参考
-
颜佳,武汉大学数字图像处理课程课件
-
DIP课堂展示
-
Tomasi C, Manduchi R. Bilateral filtering for gray and color images[C]//Computer Vision, 1998. Sixth International Conference on. IEEE, 1998: 839-846.
-
He K, Sun J, Tang X. Guided image filtering[J]. IEEE transactions on pattern analysis & machine intelligence, 2013 (6): 1397-1409.
-
Shuhang Gu, Qi Xie, Deyu Meng, Wangmeng Zuo, Xiangchu Feng & Lei Zhang. (2017). Weighted nuclear norm minimization and its applications to low level vision. International Journal of Computer Vision, 121(2), 183-208.