Histogram Equalization及其扩展

（数字图像处理的第一个作业，结果是赶着完成的，看两篇论文并且实现搞了八个小时，最后剩两个小时写报告，深深为自己英文水平着急，草草结尾还晚交了几分钟。裂开来。

1.Histogram Equalization

这个算法简称HE或者GHE(Global ~)
算法的思想非常简单，一个灰度图的直方图往往是不均匀的，这样对比度往往不高，我们要是能够使它的直方图变得更加均匀（比如每个灰度值的像素个数一样，它的对比度应该会比较好）。
下面是在网上找的一张图片以及它的直方图。

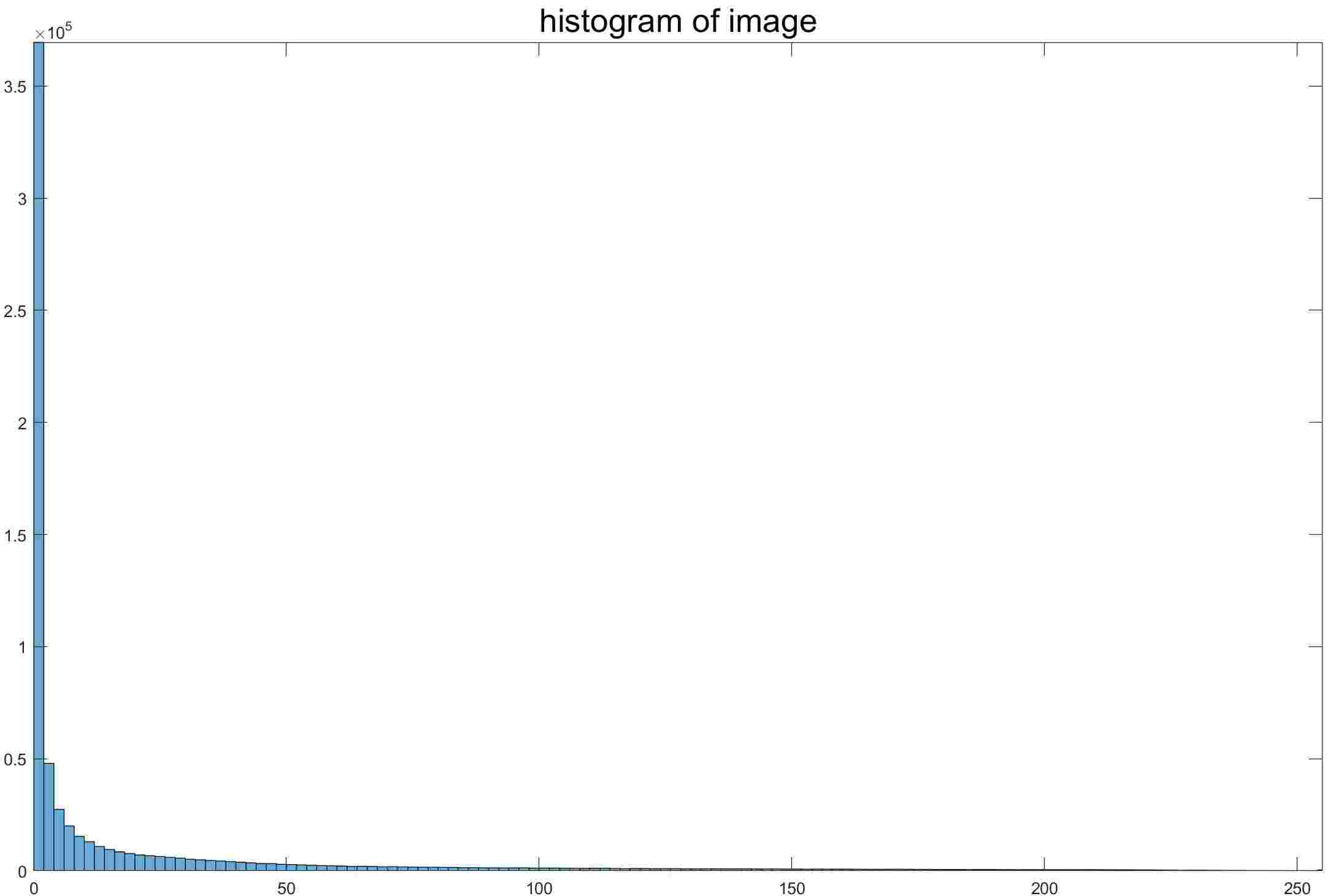
从上图的直方图中可以看到，像素的分布非常不均匀，绝大多数像素都是灰度值很小的。
通俗地讲，HE算法的思想就是让直方图中每个柱子进行不改变顺序的移动（可以合并，不能拆分），使得每个柱子的高度和它占用的灰度数相当。
从算法实现上讲，令\(cnt(i),(0\leq i\leq 255)\)表示图像每个灰度值的像素数量，\(sum(i)\)是\(cnt\)的前缀和。那么只需要把原本的灰度值\(i\)改成新的灰度值\(sum(i)*255/sum(N)\)即可。
算法的结果如下图所示

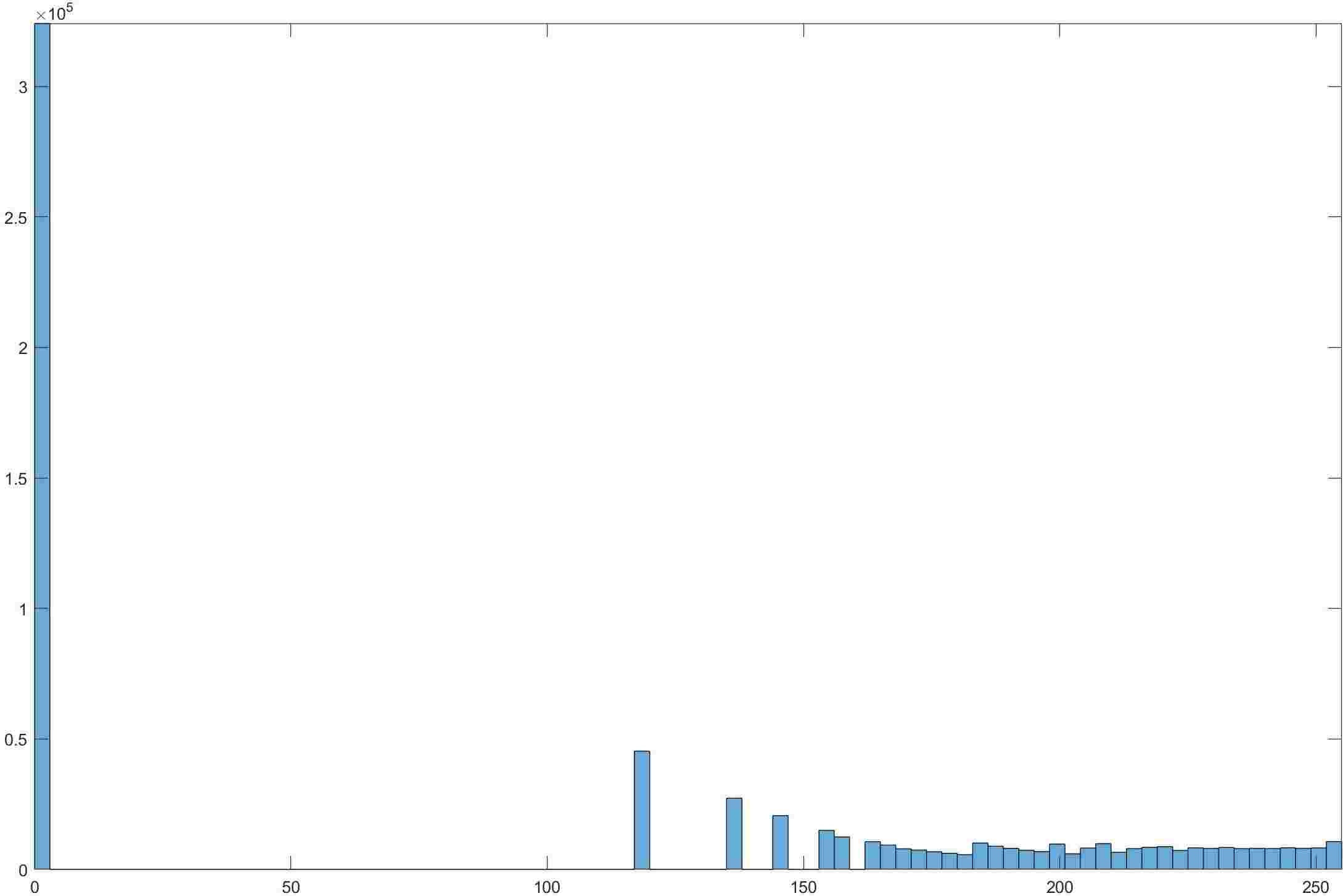
可以明显地看到直方图的柱子被移动得更均匀了，也就是柱子的高度和占的灰度数成正比了。
然而，也可以明显看到这个算法的不足，图像明暗分界处对比度被过分增强，而明和暗各自内部的对比度并没有得到很好的增强。从直方图上可以看出来，使用HE算法时，如果图像中存在非常多的某个灰度值的像素，那么就会导致非常多的灰度值不能被使用，从而有些地方对比度过大显得不自然，而有的地方对比度又没能得到很好的提高。
为了解决这个问题，我们需要找到一个把“柱子”拆分的方法。

2.Neighborhood Metrics

这一部分内容来自论文Image Contrast Enhancement using Bi-Histogram Equalization with Neighborhood Metrics
考虑如何拆分柱子，实际上就是考虑怎么给柱子里包含的像素分配权值进行一个排序，然后分配灰度值的时候就可以不用全分配一个，而且可以按照权值挨个分配更好地利用灰度值提高对比度。

2.1 Voting Metric

这是论文中提到第一个算法，很好理解，就是看自己的周围\(8\)个像素，比自己黑的有多少个，本着提高对比度的原则，周围比自己黑的越多，就应该在柱子里尽量分配更白的颜色。
可以看作每个像素有了一个权值，然后每个柱子根据权值内部排序，每个柱子最多拆分成\(9\)段（拆分效果如下图），之后再对这些拆分的柱子进行HE算法即可。

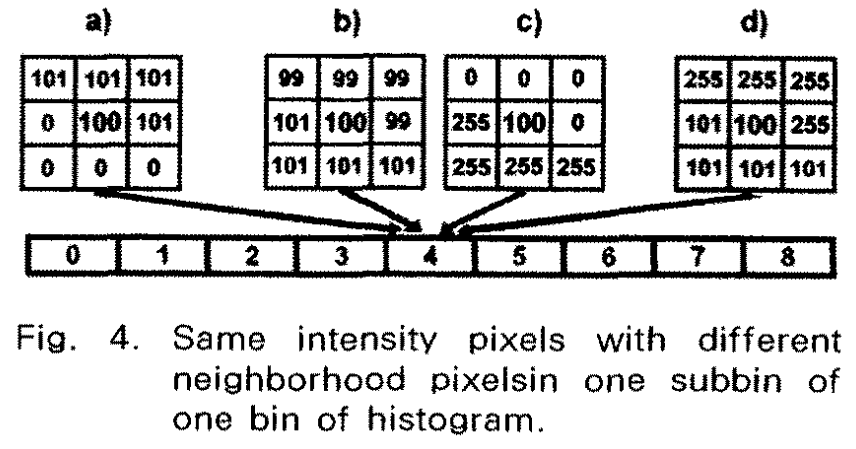
按照上述思想可以得到以下结果

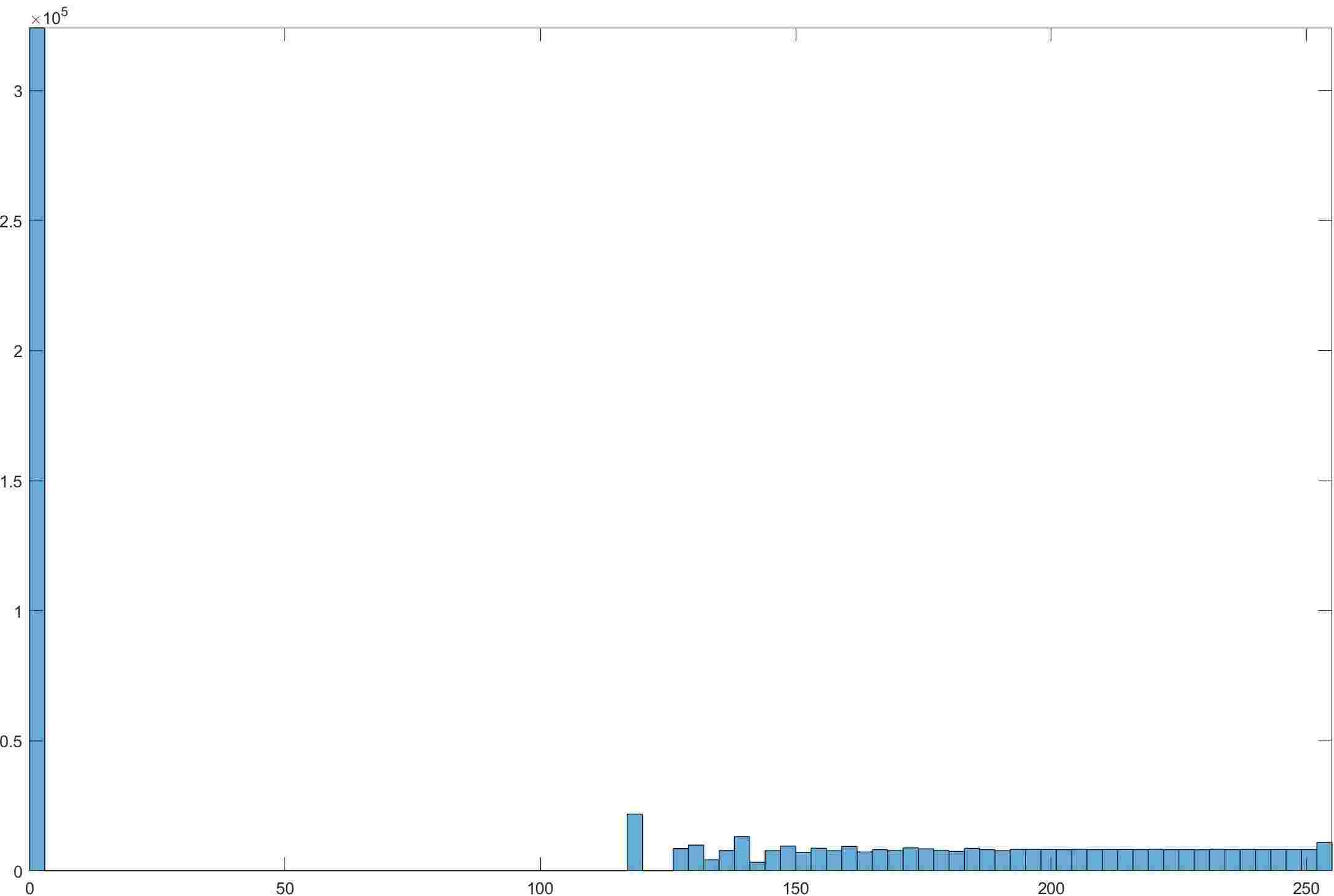
可以看到，在这幅图中，最高的柱子高度基本没变，这是因为纯黑周围不会有比它黑的，所以纯黑的柱子在这个算法下无法被拆分，还可以看到灰度值较大的区域得到了一定的平滑。不过从图片上来说没有肉眼可见变化。

2.2 Contrast Difference Metric

这个算法是在刚刚算法的基础上进行再次拆分，\(2.1\)能够把一个柱子拆成最多\(9\)个，而这个算法在刚刚拆分完的基础上再进行拆分。
这个算法是计算周围比自己灰度值小的像素平均比自己小多少，以及比自己大的像素平均比自己大多少，分别记作\(left\;average\;difference(L.a.d)\)和\(right\;average\;difference(R.a.d)\)。
设置一个阈值，当\(L.a.d<Threshold<R.a.d\)时权值设置为\(1\)，当\(L.a.d>Threshold>R.a.d\)时权值设置为\(3\)，否则为\(2\)。
拆分效果如下图所示

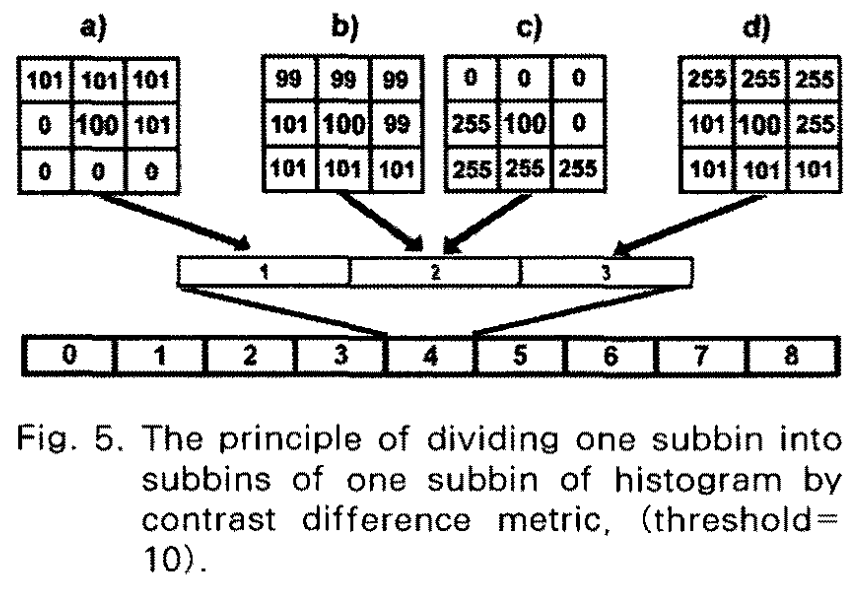
按照上述思想实现，可以得到以下结果

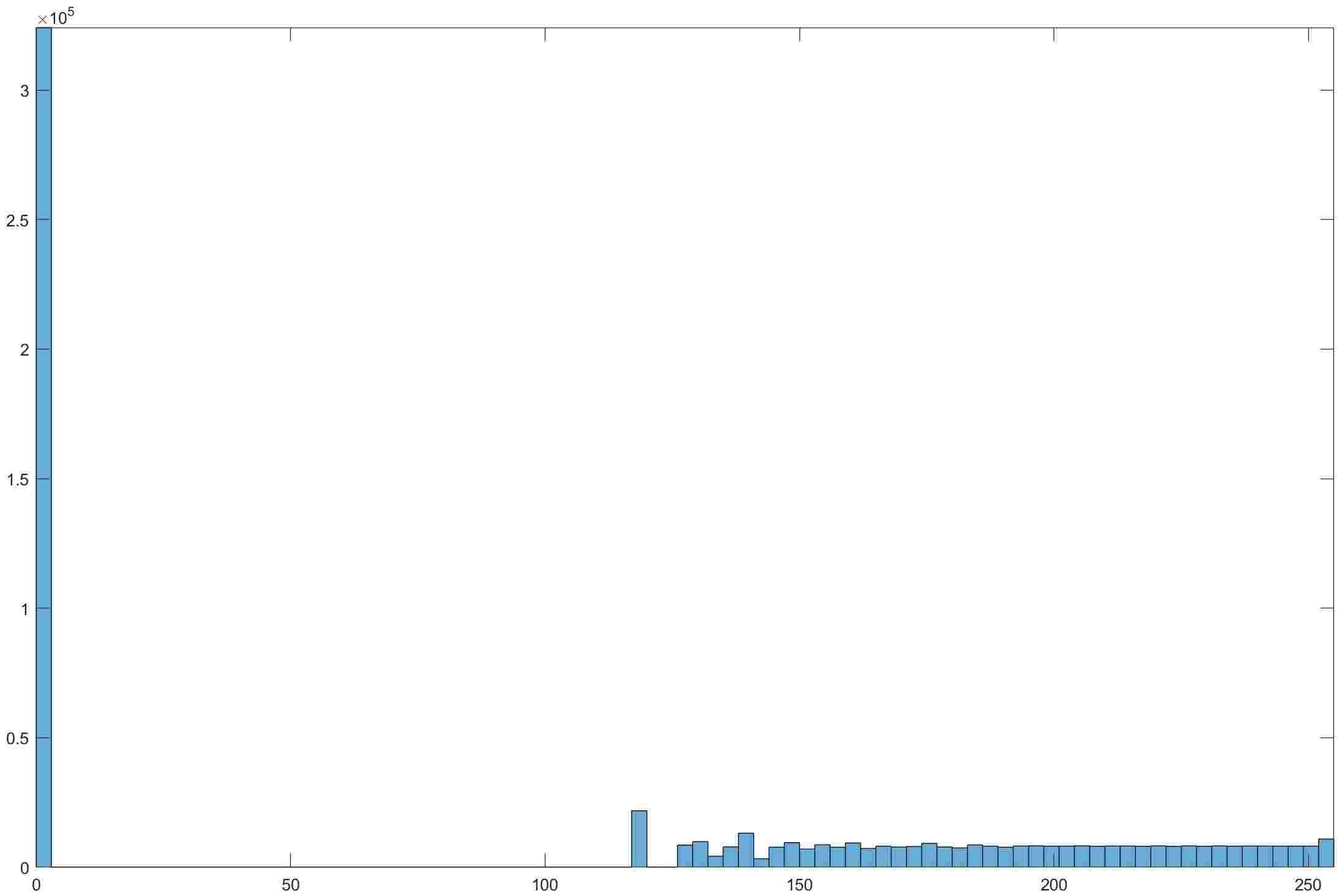
然而很不幸的是，这个改进效果甚微，几乎看不到一点差别。

2.3 Neighborhood Distinction Metric

这个算法综合了上述两个算法，给出一个更加简单的实现方式。直接给每个像素分配权值为周围灰度值比它小的像素与他差的和，这样一来一个柱子最多能够被拆分为\(2041\)个柱子了。
按照上述思想实现得到以下结果

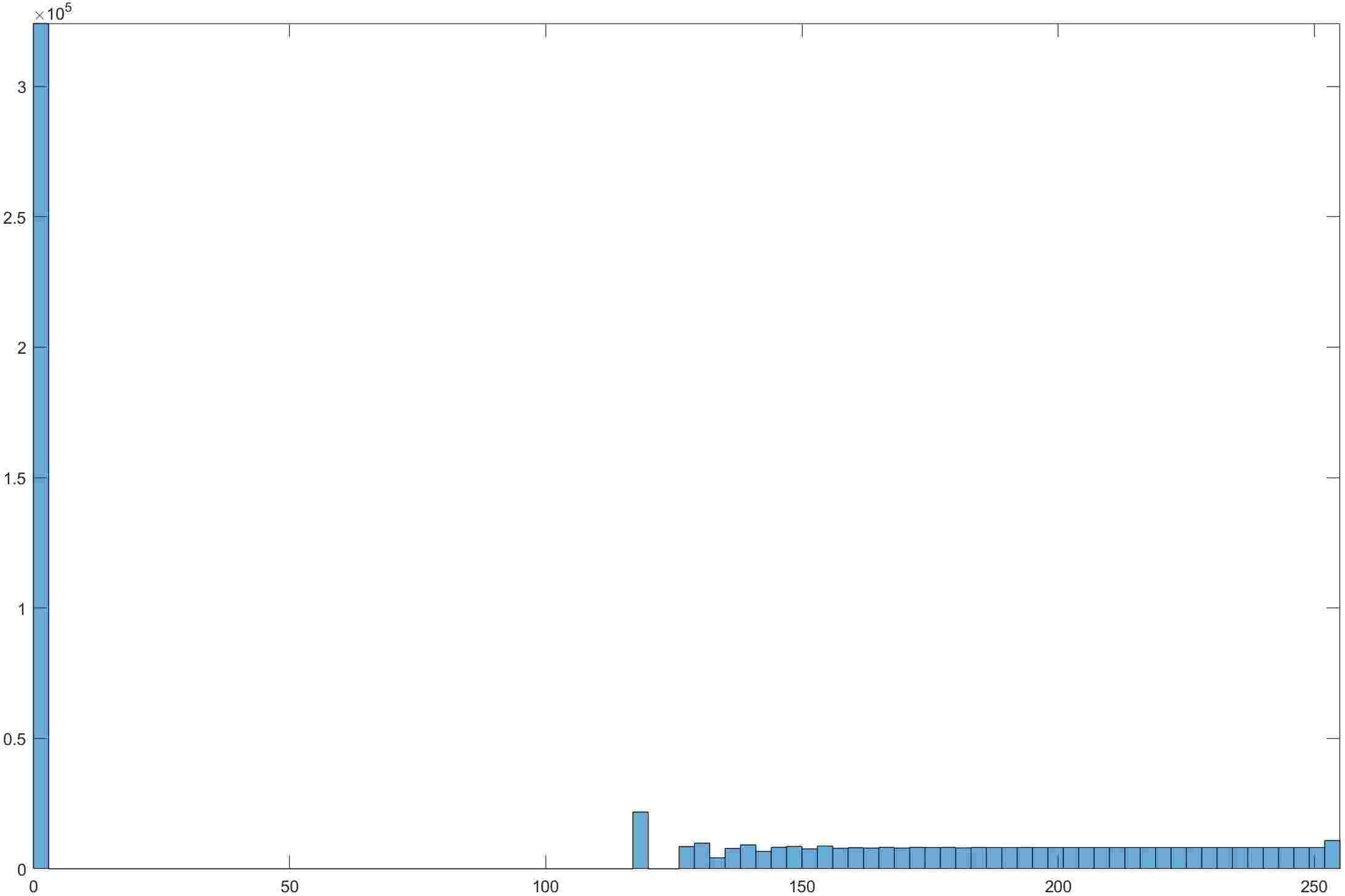
可以看到在直方图右部由于更细的拆分使得灰度分布更加的平滑了。只是在图片中依然没有太多体现。

2.4 总结

从上面可以看出，仅仅靠拆分柱子来提高对比度是不够的，当图片中某一些像素灰度值全都一样，却不表达任何意义的时候，这些像素会占用大量的灰度值区间，却不对图像效果做出贡献。为了改变这一状况，就需要把一些不重要的像素忽略，把一些重要的像素着重考虑。

3.Pixel Weight

基于\(2.4\)的思考，原本我们进行直方图统计时，一个像素算一个，并按照像素的多少来划分应该占多少灰度值。然而一副图片中可能很多像素都是没有意义的，比如一大块连续的黑色，就让他保持黑色就挺好，不需要考虑改进它的对比度。因此我们可以给像素引入权重，有的不重要的像素可以算半个甚至零个，有的很重要的像素可以算两个五个等等。于是权重的设置就成了一个研究的问题。
而且有一点很重要的是，HE以及\(2.1,2.2\)的算法和我们如何设置权值并不冲突，也就是说我们可以随意地组合拆分方法和权值方法。

3.1 Gradient

通常认为图像的边缘提供信息，于是可以考虑使用梯度作为像素的权值。拆分方式选择\(2.2\)，结果为

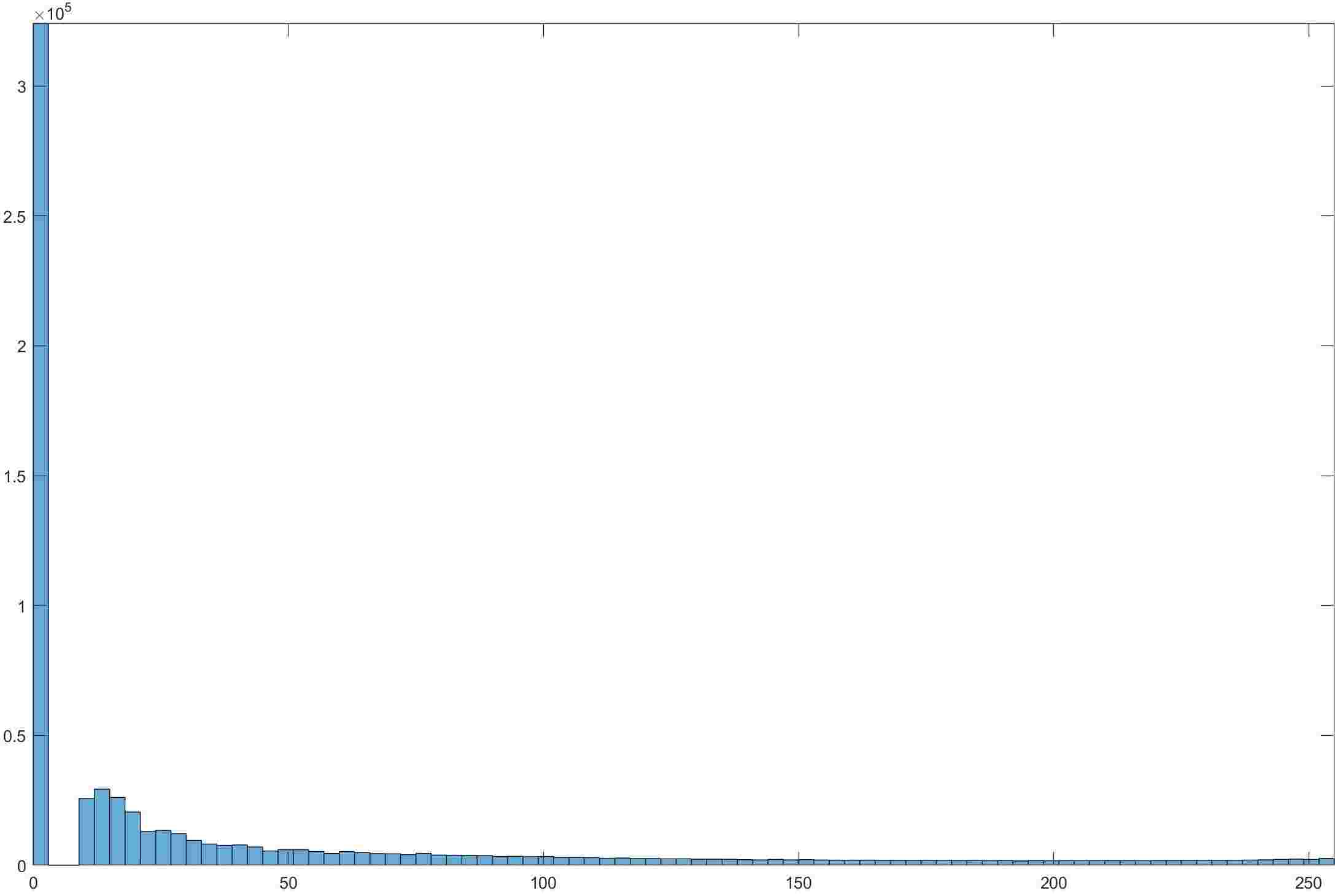
可以很明显的看到图像对比度相比之前有了较大的提升，从直方图也可以看出占有大部分像素的最高柱子不再占有大片的灰度值，这样使其他区域的对比度得到了增强。

3.2 log Gradient

这个想法是观察到有的像素梯度过大，为了抑制单个像素权值过大，我们可以使用\(\log(gradient+1)\)的方式替代梯度。结合拆分方式\(2.2\)，最后结果为

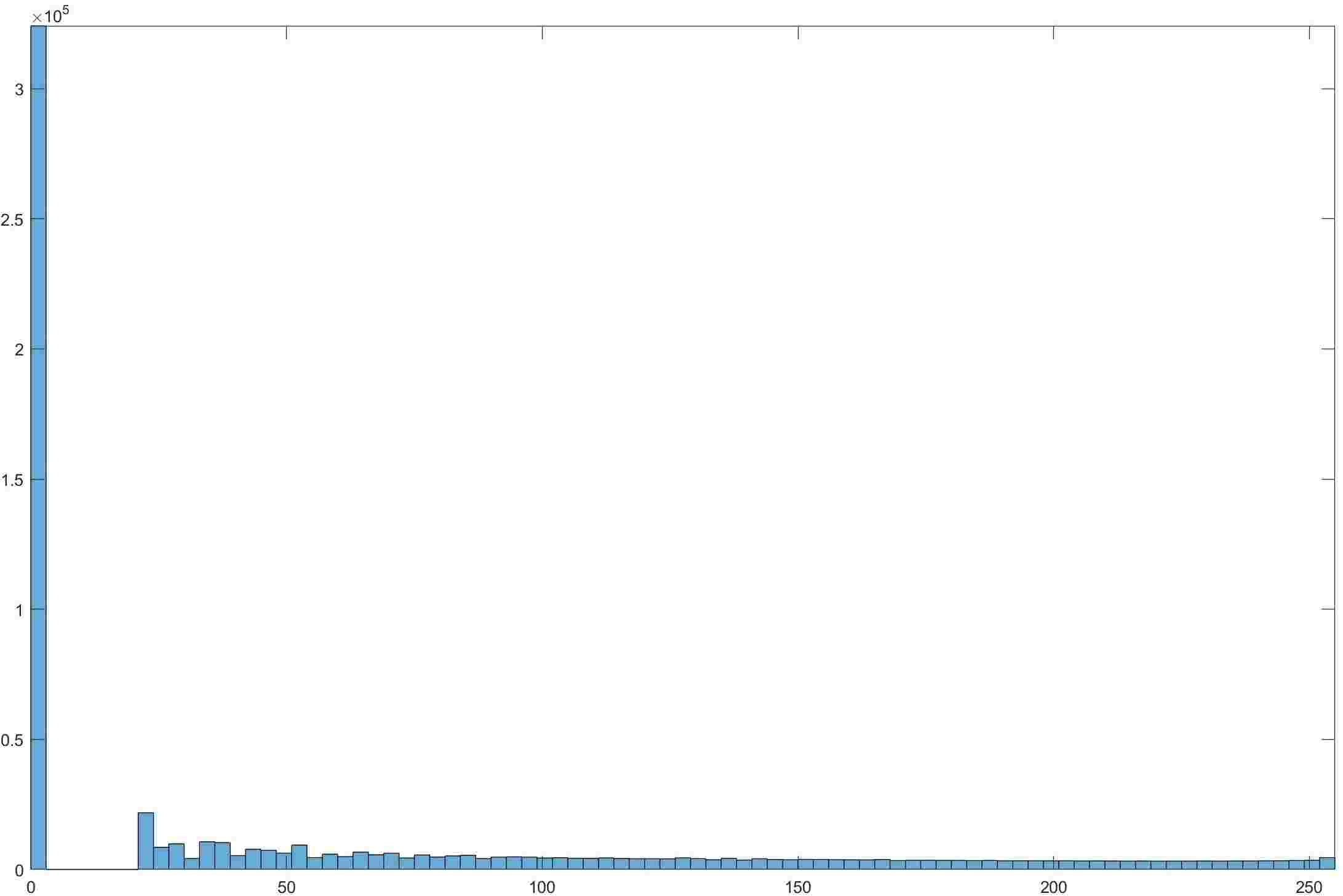
对比\(3.1\)可以发现图像整体亮度得到提高，很多原本完全看不到的细节也开始展现出来。已经达到了比较好的效果。

3.3 CONTRAST-ACCUMULATED

这个方法来自论文CONTRAST-ACCUMULATED HISTOGRAM EQUALIZATION FOR IMAGE ENHANCEMENT
实际上算法的步骤很简单：(\(S,L,\epsilon\)为预设参数)
第一步：把图片\(\mathbf A\)等比例缩放使行、列数小的为\(S\)得到图片\(\mathbf B_1\)(我写代码时直接让行数为\(S\))
第二步：把图片\(\mathbf B_1\)列数、行数除\(2\)得到\(\mathbf B_2\)，以此类推直到\(\mathbf B_L\)。
第三步：

\[\varphi_l(q)=-\sum_{q'\in \mathcal N(q)}\min\Big(\frac{\mathbf B_l(q)-\mathbf B_l(q')}{255},0\Big),(l=1,...,L)\]

其中\(q\)是图像中的二维坐标，\(\mathcal N(q)\)是\(q\)的冯诺依曼邻域，也就是曼哈顿距离为\(1\)，上下左右四个。
第四步：对\(\varphi_l(q)\)通过双三次插值变换到原图像\(\mathbf A\)的大小，记作\(\varphi_l'(x,y)\)。
第五步：权值为

\[\Phi(x,y)=\Bigg(\prod_{l=1}^L\max(\varphi_l'(x,y),\epsilon)\Bigg)^{\frac{1}{L}}\]

根据经验，\(S\)取\(256\)，\(L\)取\(4\)，\(\epsilon\)取\(0.001\)。
可以得到\(L\)个\(\varphi_l(q)\)长这样

使用这个方法结合\(2.2\)，最后结果为

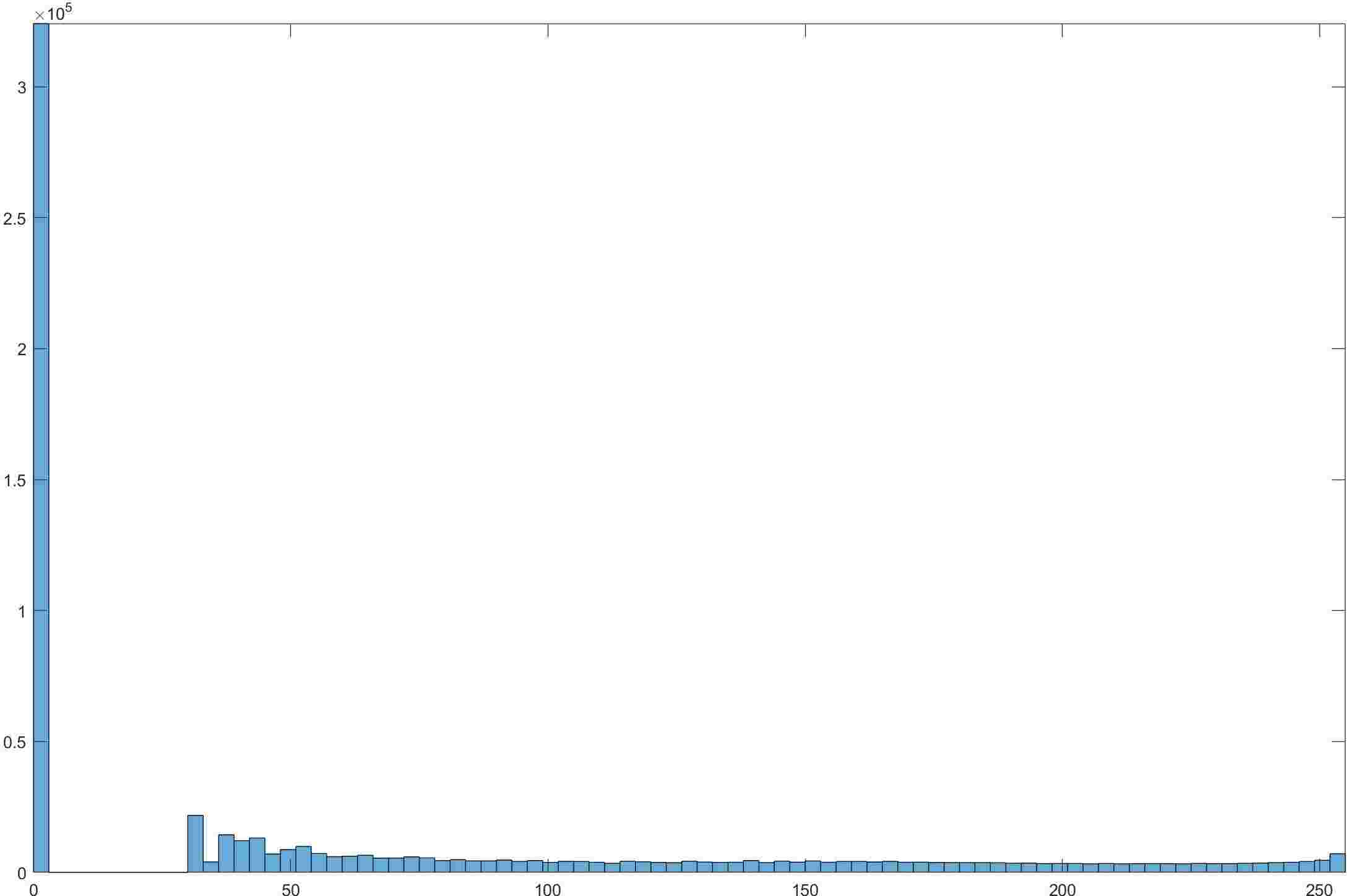
对于这幅图，该算法最终和\(3.2\)效果差不多。
还需要注意的是\(\varphi(q)\)函数的形式也是可以变换的，当前这种形式是认为某些重要的信息往往隐藏在黑色中的，如果认为重要信息往往隐藏在白色中，可以修改\(\varphi\)函数如下

\[\varphi_l(q)=\sum_{q'\in \mathcal N(q)}\max\Big(\frac{\mathbf B_l(q)-\mathbf B_l(q')}{255},0\Big),(l=1,...,L)\]

另外还有一般形式：（我脑补的，不一定正确）

\[\varphi_l(q)=\frac{\vert\mathbf B_l(q_{left})-\mathbf B_l(q_{right})\vert+\vert\mathbf B_l(q_{top})-\mathbf B_l(q_{down})\vert}{255},(l=1,...,L)\]

4.预处理

在语音信号处理中，预加重是一个常用的预处理技巧，于是我在想是不是图像也可以预加重，就是把高频分量加强，低频分量抑制。我只是做了一个简单的尝试，首先做二维傅里叶变换，然后直接根据频谱位置\(x,y\)到中心的归一化距离加上\(0.5\)作为滤波权值。
最后的对比如下图所示，左侧没有预处理，右侧是预处理后再执行算法的

可能这么对比不是很明显，但是在电脑上重合两幅图片不断切换时，能够很明显地看到右侧的图片细节部分变清晰了。可以仔细观察树干上的纹理，右侧图片的纹理是要比左侧清晰很多的。当然也有一点就是图像的噪声也被增强了，看起来的感觉就好像是：左侧的图像是右侧的图像做一个平滑滤波。
其实我也有尝试用锐化算法进行细节的增强，单看图片锐化确实能够使细节更加突出，但是会严重影响后续的对比度增强的算法效果，推测可能是因为上述频域处理比锐化卷积处理的连续性更好。此外，不仅仅是放在预处理效果不好，在将锐化作为输出图像的细节增强时，效果也不是很好，主要是对比度增强算法引入的一些没有意义的细节被放大了，比如出现一些方格。有兴趣可以自己做尝试。我使用的锐化算法比较简单。matlab代码如下

Laplace = [0 1 0;
           1 -4 1;
           0 1 0];
filter = [0 0 0; 0 1 0; 0 0 0] - 0.3 * Laplace;
img = uint8(conv2(img, filter));

5.总结

总的来说，理论上效果最好的搭配应该是：频域预处理+拆分方法\(2.2\)+权值方法\(3.3\)，但是这个方案的时间效率是比较低的。
频域预处理时间复杂度：\(O(MN\log(MN))\)
拆分\(2.1\)及\(2.2\)时间复杂度：\(O(MNm^2)\)，\(m\)是邻域统计宽度。
拆分\(2.3\)时间复杂度：\(O(MN\log(MN))\)
梯度权值及对数梯度权值时间复杂度：\(O(MNl^2)\)，\(l\)是计算梯度的卷积核大小。
CACHE时间复杂度：\(O(MNL)\)，常数比较大。
下面为使用MATLAB每种组合运行10次的总时间，单位秒，测试使用\(1023\times 682\)单通道图像。（不排除我个人代码写复杂的因素）

		拆分算法
		HE		Voting		Contrast		Neighborhood
		不处理	预处理	不处理	预处理	不处理	预处理	不处理	预处理
权值算法	全相等	0.1996	2.2534	1.2470	3.1890	3.4760	5.8460	3.1830	5.6290
	Grad	0.4920	2.6180	1.2600	3.5220	3.6800	6.2100
	logGrad	0.5970	2.8120	1.5480	3.6590	4.0660	6.2440
	CACHE	5.3010	7.7910	6.1620	7.9590	8.1010	10.5540

根据具体的场景需要可以选择不同的组合，就人眼观察感受来说，对数梯度权值加经典HE算法效果已经非常不错了，而且速度上对于1023*682的单通道图片能够达到大约每秒17帧，效果已经很不错了。如果对于一些细节部分有更高的要求可以考虑加上预处理，但是注意这样也会引入一定噪声。

6.参考

[1] Image Contrast Enhancement using Bi-Histogram Equalization with Neighborhood Metrics

[2] CONTRAST-ACCUMULATED HISTOGRAM EQUALIZATION FOR IMAGE ENHANCEMENT

7.附录

matlab代码如下所示。
其中grad,logGrad,CACHE_BP,CACHE_RG,CACHE_DP函数对输入的图片输出等尺寸的权值矩阵。
CACHE_BP,CACHE_RG,CACHE_DP函数可以传入第二个参数为ture，则该函数会显示一个四个图片的figure将算法中的\(\varphi_l\)矩阵可视化（不传入第二个参数则默认为false，不会显示）
GHE,HE_Voting,HE_Contrast,HE_Neighborhood函数均返回得出使用相应HE算法后得到的结果图片，并且可以在figure中输出显示。
GHE,HE_Voting,HE_Contrast函数第二个参数表示给每个像素设置的用来做直方图统计的权值。
GHE,HE_Voting,HE_Contrast,HE_Neighborhood函数的最后一个隐藏参数可以输入为false，表示这个函数运行不需要显示结果图片到figure（该参数默认为ture）。
代码下载：github

% main.m
clc;
clear all;
close all;

img = imread('dark_road_5.jpg');

% img = highFreqEnhance(img);

% Phi = ones(size(img));
% Phi = Grad(img);
% Phi = logGrad(img);
% Phi = CACHE_BP(img);
% Phi = CACHE_RG(img);
% Phi = CACHE_DP(img);

% pic = GHE(img, Phi);
% pic = HE_Voting(img, Phi);
% pic = HE_Contrast(img, Phi);
% pic = HE_Neighborhood(img);
% imwrite(pic, 'results/d-2.jpg');

% GHE.m
function [output] = GHE(img, Phi, Display)
%% Global Histogram Equalization
if ~exist('Display', 'var')
    Display = false;
end
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

cnt = zeros(1, 256);
[n, m] = size(img);
for i = 1 : n
    for j = 1 : m
        cnt(img(i, j) + 1) = cnt(img(i, j) + 1) + Phi(i, j);
    end
end

index = zeros(1, 256);
D = sum(cnt, 'all') / 256 + 1e-5;
j = 0;
for i = 1 :256
    index(i) = floor(j / D);
    j = j + cnt(i);
end

output = uint8(index(img + 1));

if(~Display)
    return
end

%% figure
figure;
set(gcf, 'outerposition', get(0, 'screensize'));

subplot(2, 2, 1);
histogram(img);
axis([0 255 0 inf]);
title('histogram(origin)', 'FontSize', 18);
subplot(2, 2, 3);
imshow(img);
title('image(origin)', 'FontSize', 18);

subplot(2, 2, 2);
histogram(output);
axis([0 255 0 inf]);
title('histogram(GHE)', 'FontSize', 18);
subplot(2, 2, 4);
imshow(output);
title('image(GHE)', 'FontSize', 18);

% HE_Voting.m
function [output] = HE_Voting(img, Phi, Display)
%% HE with Voting Metric
if ~exist('Display', 'var')
    Display = false;
end

if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

VotingRadius = 1;
VotingLevel = (VotingRadius * 2 + 1) ^ 2;

cnt = zeros(256, VotingLevel);
[n, m] = size(img);

Vote = ones(n, m);

for i = 1 : n
    for j = 1 : m
        for ii = max(1, i - VotingRadius) : min(n, i + VotingRadius)
            for jj = max(1, j - VotingRadius) : min(m, j + VotingRadius)
                if(img(ii, jj) < img(i, j))
                    Vote(i, j) = Vote(i, j) + 1;
                end
            end
        end
        cnt(img(i, j) + 1, Vote(i, j)) = cnt(img(i, j) + 1, Vote(i, j)) + Phi(i, j);
    end
end

index = zeros(256, VotingLevel);
D = sum(cnt, 'all') / 256 + 1e-5;
k = 0;
for i = 1 :256
    for j = 1 : VotingLevel
        index(i, j) = floor(k / D);
        k = k + cnt(i, j);
    end
end

for i = 1 : n
    for j = 1 : m
        output(i, j) = uint8(index(img(i, j) + 1, Vote(i, j)));
    end
end

if(~Display)
    return
end

%% figure
figure;
set(gcf, 'outerposition', get(0, 'screensize'));

subplot(2, 2, 1);
histogram(img);
axis([0 255 0 inf]);
title('histogram(origin)', 'FontSize', 18);
subplot(2, 2, 3);
imshow(img);
title('image(origin)', 'FontSize', 18);

subplot(2, 2, 2);
histogram(output);
axis([0 255 0 inf]);
title('histogram(HE Voting Metric)', 'FontSize', 18);
subplot(2, 2, 4);
imshow(output);
title('image(HE Voting Metric)', 'FontSize', 18);

% HE_Contrast.m
function [output] = HE_Contrast(img, Phi, Display)
%% HE with Voting Metric and contrast difference metric
if ~exist('Display', 'var')
    Display = false;
end
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

VotingRadius = 1;
VotingLevel = (VotingRadius * 2 + 1) ^ 2;

Threshold = 10;
cnt_Rank = 3;

cnt = zeros(256, VotingLevel, cnt_Rank);
[n, m] = size(img);

Vote = ones(n, m);
RVote = zeros(n, m);
Lad = zeros(n, m);
Rad = zeros(n, m);

Rank_Contrast = zeros(n, m);

for i = 1 : n
    for j = 1 : m
        for ii = max(1, i - VotingRadius) : min(n, i + VotingRadius)
            for jj = max(1, j - VotingRadius) : min(m, j + VotingRadius)
                if(img(ii, jj) < img(i, j))
                    Vote(i, j) = Vote(i, j) + 1;
                    Lad(i, j) = Lad(i, j) + img(i, j) - img(ii, jj);
                elseif(img(ii, jj) > img(i, j))
                    RVote(i, j) = RVote(i, j) + 1;
                    Rad(i, j) = Rad(i, j) + img(ii, jj) - img(i, j);
                end
                if(Vote(i, j) > 1)
                    Lad(i, j) = Lad(i, j) / (Vote(i, j) - 1);
                end
                if(RVote(i, j) > 0)
                    Rad(i, j) = Rad(i, j) / RVote(i, j);
                end
                if(Lad(i, j) < Threshold && Threshold < Rad(i, j))
                    Rank_Contrast(i, j) = 1;
                elseif(Lad(i, j) > Threshold && Threshold > Rad(i, j))
                    Rank_Contrast(i, j) = 3;
                else
                    Rank_Contrast(i, j) = 2;
                end
            end
        end
        cnt(img(i, j) + 1, Vote(i, j), Rank_Contrast(i, j)) = cnt(img(i, j) + 1, Vote(i, j), Rank_Contrast(i, j)) + Phi(i, j);
    end
end

index = zeros(256, VotingLevel, cnt_Rank);
D = sum(cnt, 'all') / 256 + 1e-5;
k = 0;
for i = 1 :256
    for j = 1 : VotingLevel
        for r = 1 : cnt_Rank
            index(i, j, r) = floor(k / D);
            k = k + cnt(i, j, r);
        end
    end
end

for i = 1 : n
    for j = 1 : m
        output(i, j) = uint8(index(img(i, j) + 1, Vote(i, j), Rank_Contrast(i, j)));
    end
end

if(~Display)
    return
end

%% figure
figure;
set(gcf, 'outerposition', get(0, 'screensize'));

subplot(2, 2, 1);
histogram(img);
axis([0 255 0 inf]);
title('histogram(origin)', 'FontSize', 18);
subplot(2, 2, 3);
imshow(img);
title('image(origin)', 'FontSize', 18);

subplot(2, 2, 2);
histogram(output);
axis([0 255 0 inf]);
title('histogram(HE Voting&Contrast Metric)', 'FontSize', 18);
subplot(2, 2, 4);
imshow(output);
title('image(HE Voting&Contrast Metric)', 'FontSize', 18);

% HE_Neighborhood.m
function [output] = HE_Neighborhood(img, Display)
%% HE with Neighborhood Metric
if ~exist('Display', 'var')
    Display = false;
end

if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

NeighborRadius = 1;

[n, m] = size(img);

pixels = zeros(n * m, 4);
cnt = 1;

for i = 1 : n
    for j = 1 : m
        s = 0;
        for ii = max(1, i - NeighborRadius) : min(n, i + NeighborRadius)
            for jj = max(1, j - NeighborRadius) : min(m, j + NeighborRadius)
                if(img(ii, jj) < img(i, j))
                    s = s + img(i, j) - img(ii, jj);
                end
            end
        end
        pixels(cnt, :) = [double(img(i, j)), double(s), i, j];
        cnt = cnt + 1;
    end
end

pixels = sortrows(pixels);

D = n * m / 256 + 1e-5;
output = uint8(zeros(n, m));
output(pixels(1, 3), pixels(1, 4)) = 0;

for i = 2 : n * m
    if(pixels(i, 1) == pixels(i - 1, 1) && pixels(i, 2) == pixels(i - 1, 2))
        output(pixels(i, 3), pixels(i, 4)) = output(pixels(i - 1, 3), pixels(i - 1, 4));
    else
        output(pixels(i, 3), pixels(i, 4)) = floor(i / D);
    end
end

if(~Display)
    return
end

%% figure
figure;
set(gcf, 'outerposition', get(0, 'screensize'));

subplot(2, 2, 1);
histogram(img);
axis([0 255 0 inf]);
title('histogram(origin)', 'FontSize', 18);
subplot(2, 2, 3);
imshow(img);
title('image(origin)', 'FontSize', 18);

subplot(2, 2, 2);
histogram(output);
axis([0 255 0 inf]);
title('histogram(HE Neighborhood Metric)', 'FontSize', 18);
subplot(2, 2, 4);
imshow(output);
title('image(HE Neighborhood Metric)', 'FontSize', 18);

% Grad.m
function [output] = Grad(img)
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

kernal1 = [1 2 1
           0 0 0
          -1 -2 -1];
kernal2 = kernal1';

dif1 = conv2(img, kernal1);
dif2 = conv2(img, kernal2);

dif1 = dif1(2:end-1, 2:end-1);
dif2 = dif2(2:end-1, 2:end-1);

output = (dif1 .* dif1 + dif2 .* dif2) .^ 0.5;

% logGrad.m
function [output] = logGrad(img)
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

kernal1 = [1 2 1
           0 0 0
          -1 -2 -1];
kernal2 = kernal1';

dif1 = conv2(img, kernal1);
dif2 = conv2(img, kernal2);

dif1 = dif1(2:end-1, 2:end-1);
dif2 = dif2(2:end-1, 2:end-1);

output = log(1 + (dif1 .* dif1 + dif2 .* dif2) .^ 0.5);

% CACHE_DP.m
function [output] = CACHE_DP(img, Display)
%% Contrast Accumulated Histogram Equalization

if ~exist('Display','var')
    Display = false;
end

if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

[n, m] = size(img);
output = ones(n, m);

L = 4;
S = 256;
eps = 1e-3;

A = cell(1, L);
phi = cell(1, L);

img = im2double(img);

for i = 1 : L
    A{i} = imresize(img, [S, round(m * S / n)]);
    S = S / 2;
end

to = [1, 0; -1 0; 0 1; 0 -1];
for l = 1 : L
    [N, M] = size(A{l});
    phi{l} = zeros(N, M);
    for i = 1 : N
        for j = 1 : M
            for k = 1 : 4
                ii = i + to(k, 1);
                jj = j + to(k, 2);
                if(ii < 1 || ii > N || jj < 1 || jj > M)
                    continue;
                end
                phi{l}(i, j) = phi{l}(i, j) - min(A{l}(i, j) - A{l}(ii, jj), 0);
            end
        end
    end
    output = output .* max(imresize(phi{l}, [n, m]), eps);
end

if(Display)
    figure;
    set(gcf, 'outerposition', get(0, 'screensize'));
    colormap('hot');
    for k = 1 : 4
        subplot(2, 2, k);
        imagesc(phi{k});
    end
end

output = output .^ (1 / L);

% CACHE_BP.m
function [output] = CACHE_BP(img, Display)
%% Contrast Accumulated Histogram Equalization
if ~exist('Display', 'var')
    Display = false;
end
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

[n, m] = size(img);
output = ones(n, m);

L = 4;
S = 256;
eps = 1e-3;

A = cell(1, L);
phi = cell(1, L);

img = im2double(img);

for i = 1 : L
    A{i} = imresize(img, [S, round(m * S / n)]);
    S = S / 2;
end

to = [1, 0; -1 0; 0 1; 0 -1];
for l = 1 : L
    [N, M] = size(A{l});
    phi{l} = zeros(N, M);
    for i = 1 : N
        for j = 1 : M
            for k = 1 : 4
                ii = i + to(k, 1);
                jj = j + to(k, 2);
                if(ii < 1 || ii > N || jj < 1 || jj > M)
                    continue;
                end
                phi{l}(i, j) = phi{l}(i, j) + max(A{l}(i, j) - A{l}(ii, jj), 0);
            end
        end
    end
    output = output .* max(imresize(phi{l}, [n, m]), eps);
end

if(Display)
    figure;
    set(gcf, 'outerposition', get(0, 'screensize'));
    colormap('hot');
    for k = 1 : 4
        subplot(2, 2, k);
        imagesc(phi{k});
    end
end

output = output .^ (1 / L);

% CACHE_RG.m
function [output] = CACHE_RG(img, Display)
%% Contrast Accumulated Histogram Equalization
if ~exist('Display', 'var')
    Display = false;
end
if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

[n, m] = size(img);
output = ones(n, m);

L = 4;
S = 256;
eps = 1e-3;

A = cell(1, L);
phi = cell(1, L);

img = im2double(img);

for i = 1 : L
    A{i} = imresize(img, [S, round(m * S / n)]);
    S = S / 2;
end

to = [1, 0; -1 0; 0 1; 0 -1];
for l = 1 : L
    [N, M] = size(A{l});
    phi{l} = zeros(N, M);
    for i = 1 : N
        for j = 1 : M
            if(i - 1 >= 1 && i + 1 <= N)
                phi{l}(i, j) = phi{l}(i, j) + abs(A{l}(i + 1, j) - A{l}(i - 1, j));
            end
            if(j - 1 >= 1 && j + 1 <= M)
                phi{l}(i, j) = phi{l}(i, j) + abs(A{l}(i, j + 1) - A{l}(i, j - 1));
            end
        end
    end
    output = output .* max(imresize(phi{l}, [n, m]), eps);
end

if(Display)
    figure;
    set(gcf, 'outerposition', get(0, 'screensize'));
    colormap('hot');
    for k = 1 : 4
        subplot(2, 2, k);
        imagesc(phi{k});
    end
end

output = output .^ (1 / L);

%highFreqEnhance.m
function [output] = highFreqEnhance(img)

if(numel(size(img)) > 2)
    img = rgb2gray(img);
end

[n, m] = size(img);

img_fft = fftshift(fft2(img));

for i = 1 : n
    for j = 1 : m
        h(i, j) = (sqrt(((i - n / 2) / n * 2) ^ 2 + ((j - m / 2) / m * 2) ^ 2) + 1) / 2;
    end
end
img_fft = abs(ifft2(fftshift(img_fft .* h)));
img_fft = img_fft - min(img_fft, [], 'all');
img_fft = img_fft ./ max(img_fft, [], 'all');

output = uint8(round(img_fft * 255));