(所有截图及部分文字出自《DeepLearning》中文版)
第一章 引言
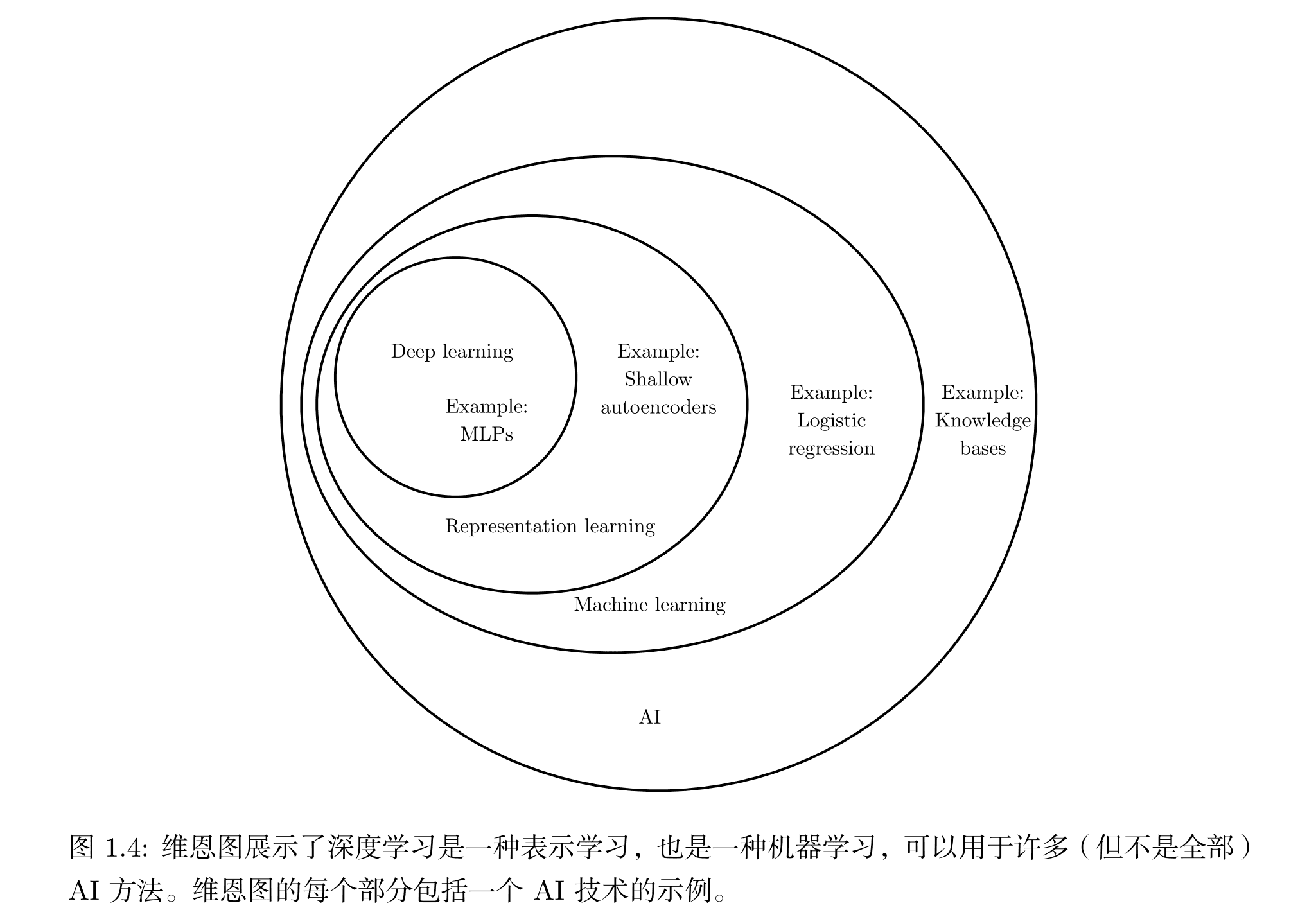
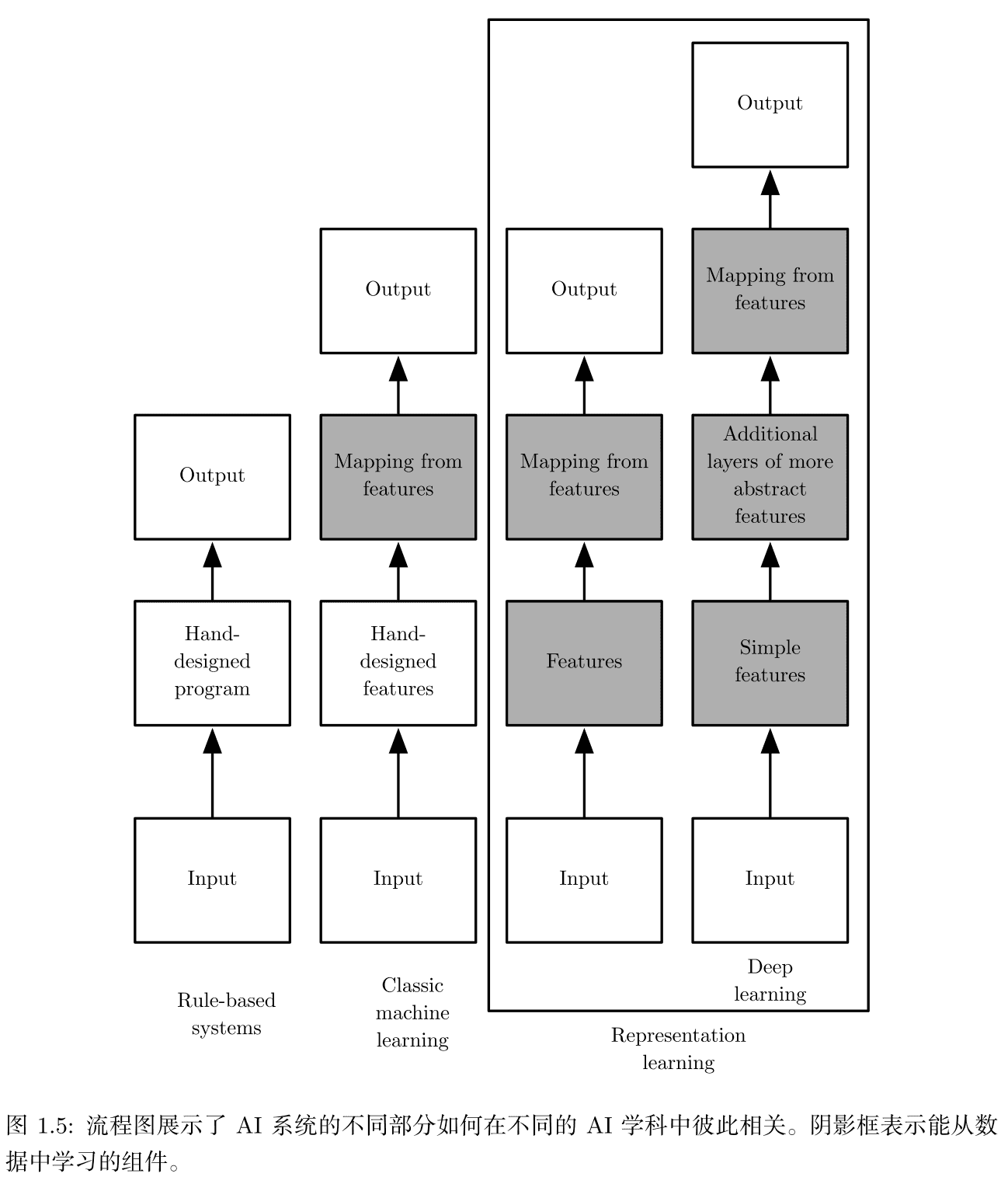
1.数据的不同表示对算法可能有较大影响

2.可通过表示学习的方法去寻找一种较好的表示方法(特征),而不是手动去找,比如深度学习可以直接输入图片它自动找到最好的特征。
第二章 线性代数
1.向量的L0范数是向量的非零元素个数,\(L_{\infty}\)范数是向量元素绝对值的最大值。

2.关于特征向量的理解
- 矩阵可以看做是向量的线性变换,对于\(n\)维非零向量\(\vec a,\vec b\),会存在线性变换(\(n\)阶方阵)\(\mathbf A\)满足
- 则矩阵\(\mathbf A\)的特征向量就可以理解为:线性变换\(\mathbf A\)只会使其进行缩放。


3.奇异值分解
- \(\mathbf A\)的奇异向量、奇异值与\(\mathbf A\mathbf A^T,\mathbf A^T\mathbf A\)的特征向量、特征值之间的关系推导:(注意\(D\)只有对角线有非零值,\(\mathbf\lambda,\mathbf\lambda'\)的非零值部分也是完全相同的)


4.Moore-Penrose伪逆


5.行列式

6.主成分分析
-
主成分分析可以将数据降维,比如将有\(n\)个变量的数据只用\(m\)个变量来表示且使其尽量不丢失信息(这是因为有的变量之间是相关的)
-
同样可以理解为一种精度损失较小的压缩方式,通过编码和解码进行转换。
-
有\(N\)个\(n\)维向量\(\vec x^{(1)}...\vec x^{(N)}\),要找到一个编码函数将每个\(\vec x^{(i)}\)编码成\(l\)维向量\(\vec c^{(i)}\)
- PCA由选定的解码函数而定。例如使用简单的矩阵乘法解码:(大一的时候就考虑过删除特征值小的特征向量进行图片压缩然而当时没有深入证明,感觉思想跟下面的差不多。)
- PCA的目标就是找到合适的编码函数使得\(\vec x^{(i)}\)与\(g(f(\vec x^{(i)}))\)尽可能接近。上述函数的求解方法如下:







一点小尝试
-
用Matlab复现奇异值分解压缩图片的想法,图片大小\(300*400\),每个像素\(8bit\),总共占用\(120KB\)
-
好的,结果惨不忍睹,本来还准备对比一下空间占用的,看来没啥意义了。当保存最大的\(50\)个奇异值及对应奇异向量时,需要空间\((300*50+50*50+50*400)*4Byte\)共\(150KB\)(假设用float4字节存实数),然而图片质量受损严重。

- Matlab代码如下:
clc;
clear all;
close all;
img = imread('food.jpg');
img = rgb2gray(img);
img = imresize(img, [300 400]);
img = im2single(img);
[U, S, V] = svd(img);
P1 = U * S * V';
left = 50;
U = U(:, 1 : left);
S = S(1 : left, 1 : left);
V = V(:, 1 : left);
P2 = U * S * V';
figure(1);
set(gcf,'outerposition',get(0,'screensize'));
subplot(1, 2, 1);
imshow(P1);
title('原图', 'FontSize', 20);
subplot(1, 2, 2);
imshow(P2);
title('压缩图', 'FontSize', 20);
第三章 概率与信息论
概念
- 可数无限多:无限多个,但是可以与自然数一一对应
- 在给定随机变量\(Z\)后,若两个随机变量\(X\)和\(Y\)是独立的,则称\(X\)和\(Y\)在给定\(Z\)时是条件独立的。
- 协方差在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度:
- 若协方差绝对值很大,则变量变化很大且同时距离各自均值的位置很远,若为正则说明倾向于同时大于或同时小于均值,若为负则说明倾向于一个大于均值另一个小于均值。 两个变量如果独立,协方差一定为零。 两个变量如果协方差为零,它们之间一定没有线性关系。
- 中心极限定理:无穷个独立随机变量的和服从正态分布
- 指数分布可以使\(x<0\)时概率为\(0\)
- Laplace分布允许我们在任意一点\(\mu\)处设置概率质量的峰值
- 分布的混合: 混合分布由一些组件分布构成。每次实验,样本是由哪个组件分布产生的取决于从一个 Multinoulli 分布中采样的结果:
- 这里\(P(c=i)\)就是选择第\(i\)个分布的概率,\(P(x\vert c=i)\)就是第\(i\)个分布。一个非常强大且常见的混合模型是高斯混合模型(Gaussian Mixture Model)它的组件\(P(x\vert c=i)\)是高斯分布。
第四章 数值计算
1.上溢和下溢
- 当接近零的数被四舍五入为零时发生下溢。当大量级的数被近似为\(\infty\)或\(-\infty\)时发生上溢。
- 在进行底层库开发时必须要考虑这些问题。

2.病态条件
- 函数输出不能对输入过于敏感,因为输入存在舍入误差。


3.Hessian矩阵



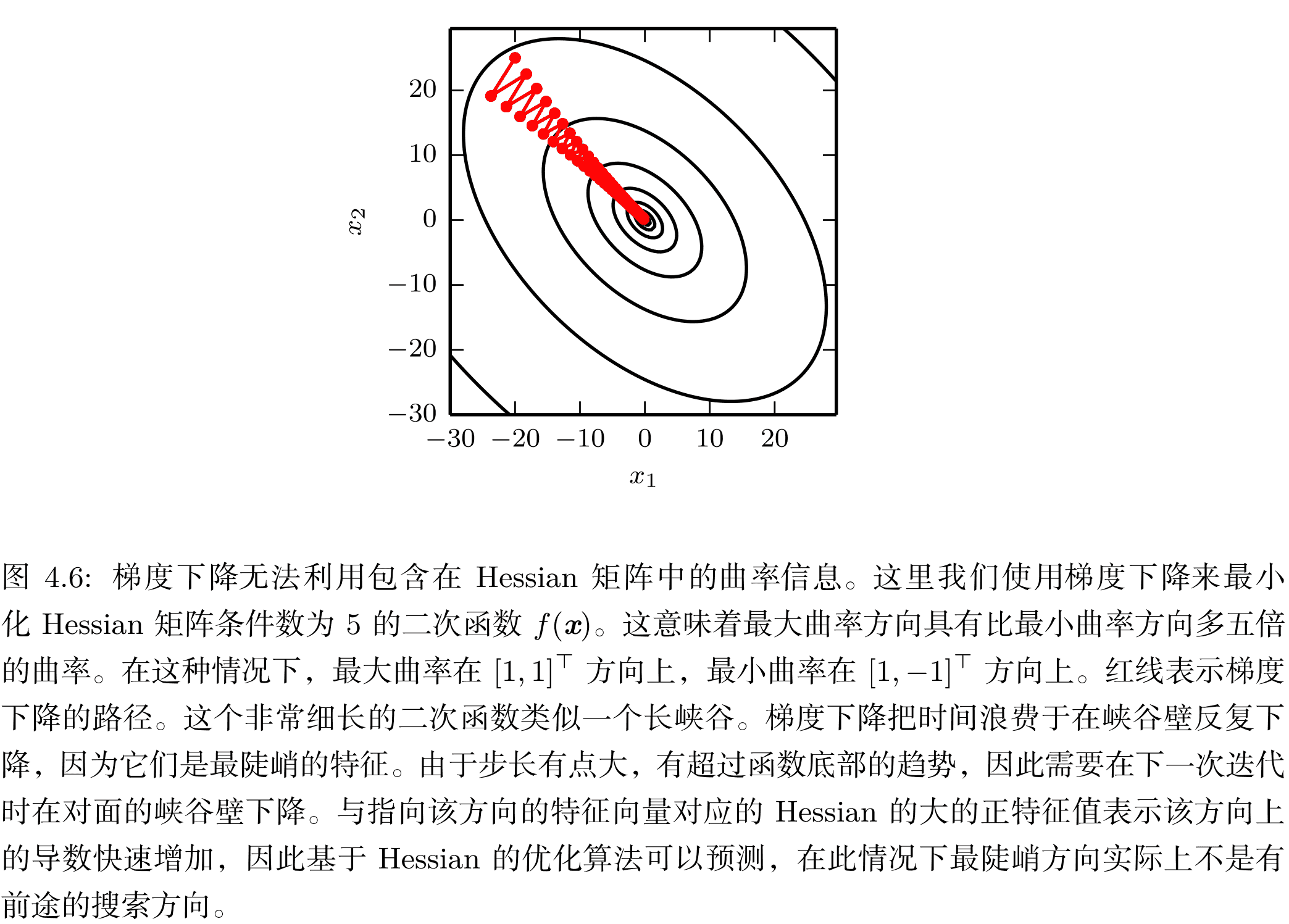
- 单纯的梯度下降无法包含Hessian的曲率信息,可能出现如下情况,最陡峭的方向并不是最有前途的下降方向,如果考虑曲率,因为最陡峭的方向梯度减少得更快,所以会对方向有一定的校正作用。
4.Lipschitz连续

第五章 机器学习基础
1.常见的机器学习任务
- 分类:\(\mathbb R^n\rightarrow\{1,...,k\}\)
- 输入缺失分类:仅需要学习一个描述联合概率分布的函数。如有两个特征输入进行分类,只需要知道联合概率分布函数\(P(Y\vert X_1,X_2)\)即可,当一个特征缺失时直接进行积分/求和即可。

- 回归:\(\mathbb R^n\rightarrow\mathbb R\)
- 转录:图片/音频\(\rightarrow\)文本

- 机器翻译:文本(语言A)\(\rightarrow\)文本(语言B)
- 结构化输出:结构化输出任务的输出是向量或者其他包含多个值的数据结构。如图像语义分割
- 异常检测:如信用卡欺诈检测,盗贼购买和卡主购买有出入,检测不正常购买行为。
- 合成与采样:如通过文本生成某个人的声音、视频游戏自动生成大型物体或风景的纹理
- 缺失值填补
- 去噪
- 密度估计/概率质量函数估计
2.无监督学习与监督学习


3.数据集表示:设计矩阵
- 当每个数据格式一致时,一般一行表示一个数据

4.估计和偏差


5.逻辑回归
-
本书的大部分监督学习算法都是基于估计概率分布\(p(y\vert \mathbf{x,\theta})\)的,算法的目的就是确定最好的参数\(\mathbf{\theta}\)
-
逻辑回归实际是用于分类而不是回归,实际是用sigmoid函数\(\sigma(x)=\frac{1}{1+\exp(-x)}\)将线性函数的输出压缩进区间\((0,1)\)。并将其解释为概率:
- 逻辑回归需要最大化对数似然来搜索最优解,可以使用梯度下降的方法。
6.支持向量机
-
支持向量机基于线性函数\(\mathbf{w}^T\mathbf x+b\),当\(\mathbf{w}^T\mathbf x+b\)为正时,预测属于正类;当\(\mathbf{w}^T\mathbf x+b\)为负时预测属于负类。
-
支持向量机的核技巧,重写线性函数为:
- 这里实际上就是通过\(\sum_{i=0}^m\alpha_i\mathbf x^{(i)}_k=\mathbf w_k\)把参数转化了一下。于是可以将\(\mathbf x\)替换为特征函数\(\phi(\mathbf x)\),也可以将点积替换为核函数
- 运算符\(\cdot\)可以是真的点积,也可以是类似点积的运算。使用核估计替换点积之后,即使用下面函数进行预测:
- 最常用的核函数是高斯核
-
其中\(N(x;\mathbf{\mu},\mathbf{\sum})\)是标准正态密度。这个核也被称为径向基函数核,因为其值沿\(v\)中从\(u\)向外辐射的方向减小。可以认为高斯核在执行一种模板匹配,训练标签\(y\)相对的训练样本\(\mathbf x\)变成了类别\(y\)的模板,当测试点\(\mathbf x'\)和模板\(\mathbf x\)的欧几里得距离很小,对应的高斯核相应很大,就说明\(\mathbf x'\)和模板\(\mathbf x\)非常相似。总的来说,预测将会组合很多这种通过训练样本相似度加权的训练标签。
-
支持向量机不是唯一可以使用核技巧来增强的算法。
-
判断新样本时,只需要计算非零\(\alpha_i\)对应的训练样本的核函数,这些训练样本被称为支持向量
7.k-最近邻
-
k-最近邻算法没有任何参数,而是一个直接使用训练数据的简单函数。当对新的输入\(\mathbf x\)进行输出时,在训练集\(\mathbf X\)上找到\(\mathbf x\)的k-最近邻,然后返回这些最近邻对应的输出值的平均值作为\(\mathbf x\)的输出。
-
可以看出该算法对每一个特征的重要性没有很好的划分,如果有很多维的特征而只有少数影响到结果,那么这种方法的输出会受到大多数的不相关特征的严重影响。
8.决策树
-
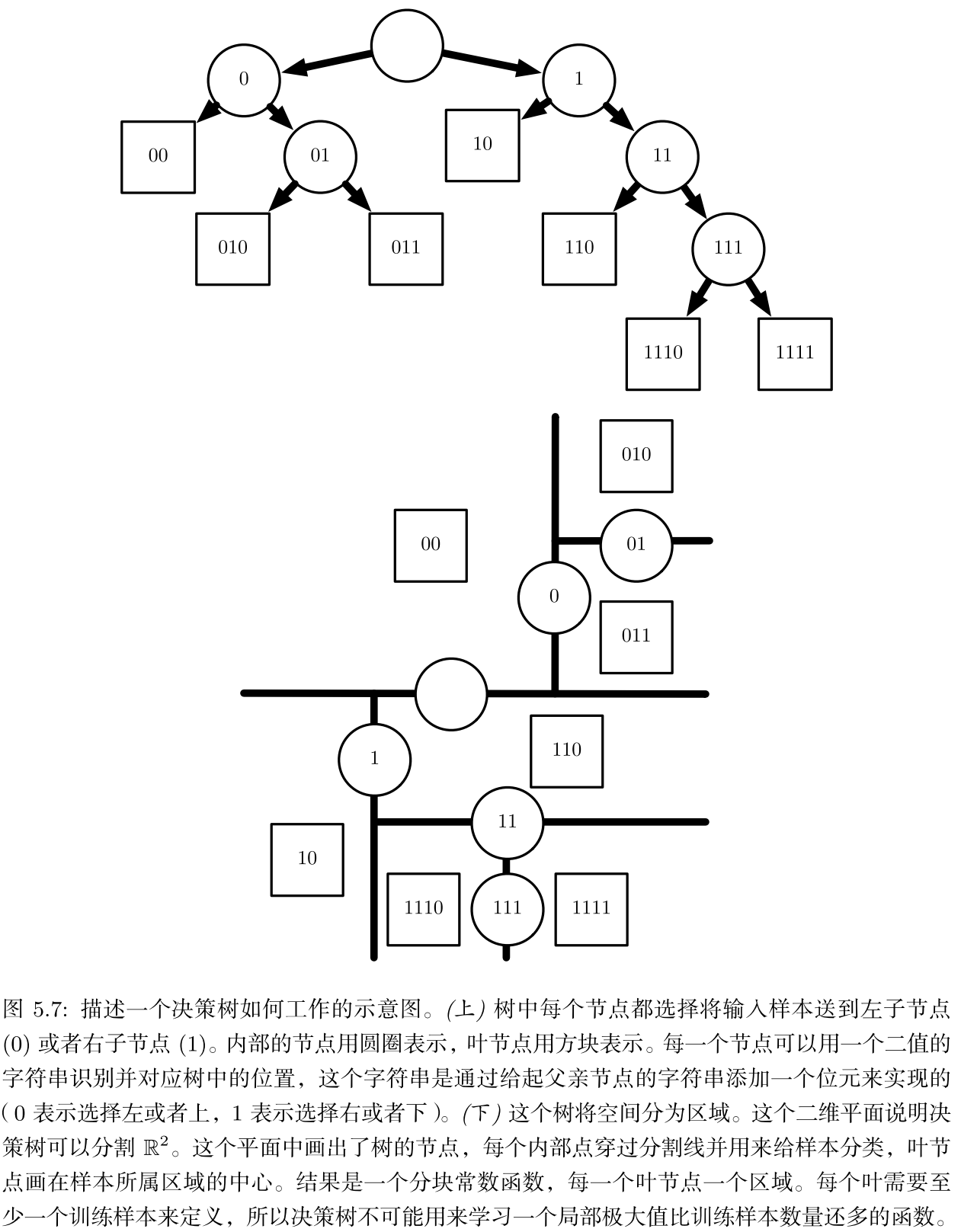
决策树及其变种是另一类将输入空间分成不同的区域,每个区域有独立参数(停顿)的算法。
-
下图是一个例子,决策树可以把二维平面不停地按照一分为二划分,当一个区域里输出都相同的时候停止划分。
-
然而对于简单的二分类:\(x_1>x_2\)时为正类
-
决策树会需要不停地划分空间,就像是要用平行于坐标轴的线段去把直线\(y=x\)画出来。
9.再讲主成分分析
-
在第二章已经提到过主成分分析法的压缩数据的应用,我们也可以将其看做学习数据表示的无监督学习算法。
-
PCA的作用就是要使原始数据表示\(\mathbf X\)去相关。
-
假设有设计矩阵\(\mathbf X_{m×n}\),减去均值使得\(\mathbb E[\mathbf x]=0\)(个人理解是每一列减去每一列的均值),\(\mathbf X\)对应的无偏样本协方差矩阵如下
-
注意上述协方差矩阵是\(n×n\)的矩阵
-
PCA通过线性变换找到一个\(Var[\mathbf z]\)是对角矩阵的表示\(\mathbf z=\mathbf W^T\mathbf x\)
-
在第二章中有:
- 再结合前面特征分解或奇异值分解的知识,不难得出
- 要使$\mathbf z$各个维度无关,只需要令$\mathbf W=\mathbf V$即可,即有$Var[\mathbf z]=\frac{1}{m-1}\mathbf \Sigma^2$
10.k-均值聚类
-
首先确定\(k\)个不同的中心点,然后对每一个样本找最近作为分类,然后同一类样本的取均值作为中心点,按照前述不断迭代直到收敛。
-
聚类算法的问题在于不知道聚出来的结果到底是什么意义。
11.随机梯度下降
- 随机梯度下降的核心是,梯度是期望。期望可以使用小规模的样本近似估计,因此在算法的每一步可以从训练集中抽取小批量样本,通常数量在几百以内。